Как склеить додекаэдр

Содержание

Инструкция

1
Распечатайте шаблон додекаэдра на принтере. Вырежьте фигуру из выкройки. Аккуратно загните места сгибов с помощью линейки и последовательно склейте. Наносить клей надо на «лепестки», которые скрепляются друг с другом, а не на всю грань додекаэдра. Чтобы готовая фигура выглядела привлекательно, cлегка продавите места сгибов тыльной стороной ножа, а погрешности, срезы или потертости закрасьте маркером или фломастером.
2
Если у вас нет принтера, изготовьте шаблон додекаэдра самостоятельно, с помощью транспортира. Начните с построения центрального пятиугольника. Чтобы правильно построить пятиугольник, помните, что угол между двумя его сторонами составляет 108°.
3
К каждой стороне получившейся фигуры пририсуйте по пятиугольнику тех же размеров. Всего должно получиться 6 пятиугольников — своеобразный цветок с лепестками. Проделайте то же самое еще раз, не забывая, что необходимо соединить «лепестки» двух «цветков» по стороне.
4
Обязательно сделайте по сторонам небольшие припуски для смазывания их клеем. Затем вырежьте, согните места сгибов и склейте. По желанию можете обернуть додекаэдр в цветную бумагу, наклеив ее на фигуру, или раскрасить многогранник.
5
Если вы захотели склеить додекаэдр, а клея под рукой не оказалось, сделайте надрезы по линиям сгибов до середины сгиба против часовой или по часовой стрелке — так, как вам наиболее удобно. Затем просто вставьте стороны будущего додекаэдра по надрезанным граням друг в друга, они будут достаточно надежно держаться.
6
Еще один способ изготовить додекаэдр — сделать его макет в технике оригами. В качестве помощника используйте видео-инструкцию из интернета. Потребуется 30 листов бумаги, будет красивее, если использовать цветную бумагу. Возьмите один лист и сложите его пополам. Затем согните половинки листа еще пополам в обратные стороны, так, чтобы получилось три линии сгиба и фигура в виде веера.
7
После этого заверните каждую сторону под прямым углом, модуль сложите наискосок. То же самое сделайте с другими двумя листами. Эти три модуля — первая вершина додекаэдра. Из 27 листов сделайте оставшиеся модули по описанному выше принципу, вложите модули друг в друга

Получится эффектный додекаэдр-оригами.
Обратите внимание
Оптимальная плотность бумаги для изготовления додекаэдра — 220 г/м?. Более тонкая бумага мнется в процессе работы, а совсем толстая — ломается по сгибам.
Полезный совет
В процессе сборки додекаэдра-оригами закрепляйте модули скрепками или проклеивайте места соединения, так как они могут развернуться — устойчивой фигура становится только в конце изготовления.

Внимание, только СЕГОДНЯ!

Геометрические свойства

Древние мудрецы утверждали: «Чтобы понять невидимое, внимательно смотри на видимое». В сакральных науках додекаэдр считается самым мощным и интересным многогранником. Впервые объемный двенадцатигранник был сделан и построен древнегреческим ученым Теэтетом в IV веке до нашей эры.

Фигура состоит из следующих элементов:

12 граней — правильных пятиугольников;
30 ребер;
20 вершин, в каждой из которых находится точка пересечения трёх ребер и вершина трёх пятиугольников.

Любая из 15 плоскостей симметрии также проходит во всех гранях через середину и вершину противоположно расположенного ребра.

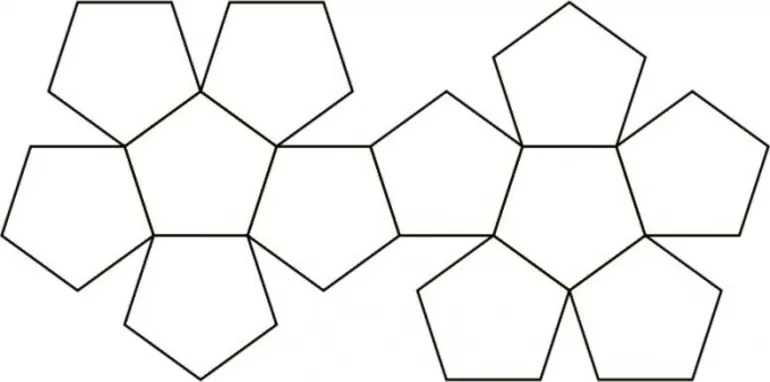
Чтобы понять, что собой представляет этот геометрический элемент, можно сделать развертку додекаэдра. Так более понятно выглядит его площадь. Кроме того, именно по этой схеме можно пошагово сделать фигуру самостоятельно из бумаги или картона, начертив предварительный шаблон с небольшими припусками для загибов.

На чертеже важно правильно определить линии сгибов. При этом немаловажно перед склеиванием знать, какой оттенок материала будет использован

По мнению древнегреческого философа Платона, додекаэдр не относится к известным земным элементам (Огонь, Вода, Земля) и поэтому ассоциируется с пустотой. Такая фигура делается из бумаги желтого цвета.

Развертка также может быть цветной. Первый классический вариант сборки — фигура с гранями, каждая из которых имеет свой оттенок. Второй способ — использование повторяющихся цветов, но они не могут граничить друг с другом.

Додекаэдр, ассоциирующийся с формой кристалла, имеет следующие характерные для него свойства и элементы симметрии:

присутствует 6 осей пятого порядка (это означает, что фигура поворачивается на угол 72 градуса — 360/5);
15 осей второго порядка (при симметричном повороте угол составляет 360/2 = 180 градусов);
10 осей третьего порядка (симметрия проявляется при повороте на 120 градусов — 360/3).

Идея определения симметрии проста и интересна: если внутри кристалла вообразить ось, а потом вокруг нее повернуть фигуру на определенный угол, то элемент сам с собой совпадет. Это не свойственно никаким другим геометрическим фигурам.

Кусудама из правильных пятиугольников

Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.

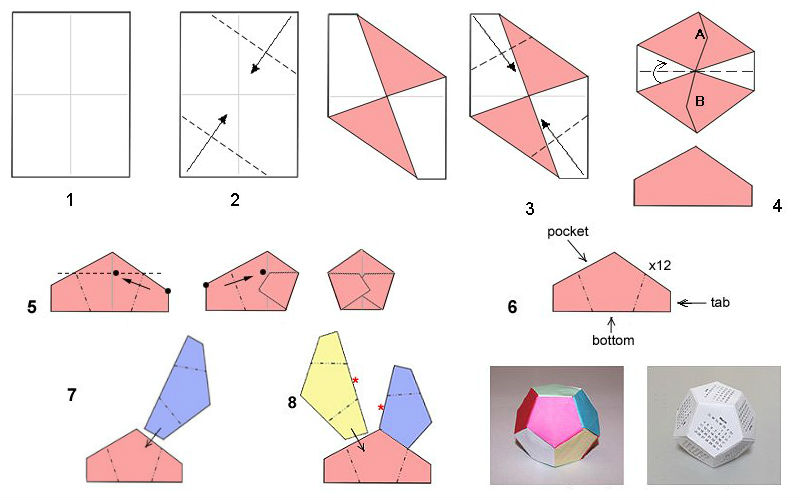
Пошаговая инструкция:

Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
Аналогично складываем противоположные углы.
Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
Продолжаем сборку, пока не используем все 12 модулей.

Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.

Разузнай! – Додекаэдр – Как сделать правильный додекаэдр своими руками – Как сделать звездчатый додекаэдр – Разузнай!

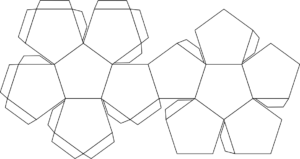
Додекаэдром называется правильный многогранник, составленный из двенадцати правильных пятиугольников. Эта эффектная объемная фигура обладает центром симметрии, называемым центром додекаэдра.

Кроме того, в ней присутствуют пятнадцать плоскостей симметрии (в каждой грани любая из них проходит через середину противоположного ребра и вершину) и пятнадцать осей симметрии (пересекающих середины параллельных противолежащих ребер).

Каждая из вершин додекаэдра является вершиной трех пятиугольников правильной формы.

Свое название конструкция получила по количеству входящих в нее граней (традиционно древние греки давали многогранникам имена, отображающие число граней, составляющих структуру фигуры). Таким образом, понятие «додекаэдр» образовано из значений двух слов: «додека» (двенадцать) и «хедра» (грань).

Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и икосаэдром).

Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.

Правильные многогранники всегда привлекали людей своей красотой, органичностью и необыкновенным совершенством форм, но додекаэдр имеет особую историю, которая из года в год обрастает все новыми, иногда совершенно мистическими, фактами.

Представители многих цивилизаций усматривали в нем сверхъестественную и таинственную сущность, утверждая, что: «Из числа двенадцать произрастает многое». На территориях древних разрушенных государств до сих пор находят маленькие фигурки в виде додекаэдров, выполненные из бронзы, камня или кости.

Кроме того, при раскопках на землях современной Англии, Франции, Германии, Венгрии, Италии археологи обнаружили несколько сотен так называемых «римских додекаэдров», датирующихся II-III-м веками нашей эры. Основные размеры фигурок составляют от четырех до одиннадцати сантиметров, причем отличаются они самыми невероятными узорами, текстурами и техникой исполнения.

Как сделать правильный додекаэдр своими руками

Сегодня конструкция данной фигуры нашла свое отображение во многих вариантах художественного творчества, архитектуре и строительстве.

Народные умельцы изготавливают из цветной или белой бумаги необыкновенные по красоте оригами в виде ажурных додекаэдров, а из картона делают оригинальные и прочее).

В продаже можно приобрести уже готовые наборы, содержащие все необходимое для изготовления сувениров, но наиболее интересно произвести весь процесс работы своими руками, начиная от построения отдельных деталей и заканчивая сборкой готовой конструкции.

Для того, чтобы сделать правильный додекаэдр из картона, необходим собственно сам материал и подручные средства:

ножницы,
карандаш,
ластик,
линейка,
клей.

Хорошо иметь тупой нож или какое-либо приспособление для загибания припусков, но если их нет, то вполне подойдет металлическая линейка или те же ножницы.

Делаем правильный додекаэдр

1. Самый первый этап в изготовлении – построение пятиугольника нужного размера. Должен получиться вот такой элемент. Он и станет основой фигуры.
Далее конструируете развертку додекаэдра с учетом припусков на склеивание.
В результате получится «выкройка» приблизительно такого вида. Варианты могут различаться, если припуски будут другой формы или размещены на других гранях.
Аккуратно по линиям сгибаете припуски.
Склеиваете.
Наносите на готовый додекаэдр нужный рисунок или декорируете другим выбранным способом.

Готово!

Как сделать звездчатый додекаэдр

Звездчатые додекаэдры имеют более сложную конструкцию по сравнению с обычными. Эти многогранники подразделяются на малый (первого продолжения), средний (второго продолжения) и большой (последняя звездчатая форма правильного додекаэдра). Каждый из них отличается своими особенностями построения и сборкой.

Для работы Вам потребуются те же материалы и инструменты, что и для изготовления стандартного додекаэдра.

Если Вы решили сделать первый вариант (малый додекаэдр), то необходимо построить чертеж первого элемента, который станет основой для всей конструкции (в дальнейшем производится ее склеивание или сборка деталей при помощи скрепок).

Делаем звездчатый додекаэдр

Строите схему основной детали нужных размеров с необходимыми припусками. Должен получиться приблизительно такой элемент.
По обозначенным линиям сгибаете, в том числе не забываете о припусках.
Склеиваете каждую деталь по отдельности.
Собираете додекаэдр полностью.
Раскрашиваете или наносите любое из выбранных изображений.

Готово!

Список литературы

Инженерная 3D-компьютерная графика: учебник и практикум для академического бакалавриата / А.Л. Хейфец, А.Н. Логиновский, И.В. Буторина, В Н. Васильева; под ред. А.Л. Хейфеца. – 3-е изд., перераб. и доп. – М.: Изд-во Юрайт, 2015. –602 с.
Шаль М. Исторический обзор происхождения и развития геометрических методов. Т. 2. Гл.1 § 1-8 – М.: Моск. мат. о-во, 1883. – 748 c. http://bookre.org/reader?file=444142&pg=2
Кольман Э. История математики в древности. М.: Государственное издательство физико-математической литературы, 1961. – 235 с. http://www.mathedu.ru/lib/books/kolman_istoriya_matematiki_v_drevnosti_1961/
Мартыненко Г.Я. Математика Гармонии: Возрождение (XIV–XVI вв.) (к 500–летию книги Луки Пачоли «О божественной пропорции») // Академия тринитаризма, (эл № 77-6567, публ.16006, 20.07.2010). http://www.trinitas.ru/rus/doc/0016/001c/1679-mrt.pdf
Стахов А.П. Математика гармонии: Инновации в информационных технологиях, в основаниях математики, в образовании. // Интернет-журнал Науковедение. М.: ИГУПИТ, №4, 2012. – С. 98. https://naukovedenie.ru/PDF/33tvn412.pdf
Крайнева Л.Б. Методика проведения спецкурса по геометрии для старшеклассников в условиях личностно-ориентированного обучения: дис. …канд. пед. наук. М., 2007. – 260 с. http://www.dissercat.com/content/metodika-provedeniya-spetskursa-po-geometrii-dlya-starsheklassnikov-v-usloviyakh-lichnostno-
Короев Ю.И. Начертательная геометрия. М.: КноРус, 2015. –422 с.
Divina proportione: opera a tutti glingegni… : Internet Archive Электронный ресурсhttps://archive.org/details/divinaproportion00paci/page/n41
Щетников А. И. Лука Пачоли и его трактат «О божественной пропорции» // Математическое образование, №1 (41), 2007. – С. 33–44. http://www.nsu.ru/classics/pythagoras/Pacioli.pdf
Ливио М. φ – Число Бога. Золотое сечение – формула мироздания: АТС, М., 2015. – 218 с. http://zodorov.ru/mario-livio—chislo-boga-zolotoe-sechenie—formula-mirozdaniy.html?page=7
Наука. Величайшие теории: выпуск 14: Трехмерный мир. Евклид. Геометрия. – М. Де Агостини, 2015. – 168 с. https://coollib.com/b/337501/read
Смирнова И.М. Каскады из правильных многогранников http://www.vasmirnov.ru/Lecture/Kaskady/Kaskady.htm
Гарднер М. Математические головоломки и развлечения: гл. 23 – М.: Мир, 1971. – 511 с. http://mathemlib.ru/books/item/f00/s00/z0000043/st025.shtml
Долбилин Н.П. Три теоремы о выпуклых многогранниках // Квант, №5, 6, 2001. –С.7-12. http://kvant.mccme.ru/pdf/2001/05/kv0501dolbilin.pdf
Долбилин Н.П., Канель А.Я. Гармония правильных многогранников. Математические этюды, 2002-2019. http://www.etudes.ru/ru/etudes/platonic-solids-harmony/
Бездетко П.В. и др. Пространственное моделирование твердотельных правильных многогранников (тел Платона) в системе AutoCAD // Наука и прогресс транспорта. Вестник Днепропетровского национального университета железнодорожного транспорта, – 2009, –№ 27, — С. 167-170. https://cyberleninka.ru/article/n/prostranstvennoe-modelirovanie-tverdotelnyh-pravilnyh-mnogogrannikov-tel-platona-v-sisteme-autocad

Тонкости работы

Построить разверту многогранника и склеить из нее бумажную модель — дело тонкое. Развертку, конечно, можно взять уже готовую. А можно, приложив услилия, построить ее самостоятельно. Но чтобы сделать полноценную объемную модель многогранника, нужно ее собрать. Многогранник лучше всего делать из плотной бумаги, которая хорошо держит форму и не коробится от клея. Все линии, которые необходимо согнуть, лучше всего предварительно продавить, используя, например, непишущую шариковую ручку или обратную сторону лезвия ножа. Этот нюанс поможет сложить модель аккуратнее, с соблюдением размеров и направлений ребер.

Если сделать разные многогранники из цветной бумаги, то такие модели можно использовать в качестве декоративных элементов, украшающих помещение — детскую комнату, кабинет, гостиную. Кстати, многогранники можно назвать уникальной находкой декораторов. Современные материалы позволяют на основе геометрических фигур создавать оригинальные предметы интерьера.

Бумажные поделки — это не только различные открытки и аппликации, выполненные в виде плоских изделий. Очень оригинальными получаются объемные модели фигур (фото 1). Например, можно сконструировать Рассмотрим некоторые способы его выполнения, используя схемы и фотографии.

Геометрические отношения

Додекаэдра является третьим в бесконечном множестве усеченного trapezohedra которая может быть построена путем усечения двух осевых вершин пятиугольного трапецоэдра .

В созвездиях регулярного додекаэдра составляют три из четырех Кеплер-Пуансо многогранников .

Выпрямляются додекаэдр образует икосододекаэдр .

Правильный додекаэдр имеет икосаэдрическую симметрию I _h , группу Кокстера , порядок 120, с абстрактной групповой структурой A ₅ × Z ₂ .

Отношение к правильному икосаэдру

Когда правильный додекаэдр вписан в сферу , он занимает больше объема сферы (66,49%), чем икосаэдр, вписанный в ту же сферу (60,55%).

Правильный додекаэдр с длиной ребра 1 имеет более чем в три с половиной раза объем икосаэдра с такой же длиной ребер (7,663 … по сравнению с 2,181 …), что примерно составляет 3,512 461 179 75 , или в точных терминах:35(3 ϕ + 1) или (1,8 ϕ + 0,6) .

У правильного додекаэдра 12 граней и 20 вершин, а у правильного икосаэдра 20 граней и 12 вершин. У обоих по 30 ребер.

Отношение к вложенному кубу

Куб может быть встроен в правильный додекаэдр, прикрепленный к восьми из его равноудаленных вершин в пяти различных положениях. Фактически, пять кубов могут перекрываться и сцепляться внутри правильного додекаэдра, в результате чего получается соединение пяти кубов .

Отношение ребра правильного додекаэдра к ребру куба, вложенного внутрь такого правильного додекаэдра, равно 1: ϕ или ( ϕ — 1): 1.

Отношение объема правильного додекаэдра к объему куба, заключенного внутри такого правильного додекаэдра, равно 1: 22 + ϕ, или 1 + ϕ2 : 1 или (5 + √ 5 ): 4.

Например, вложенный куб с объемом 64 (и длиной ребра 4) будет вложен в правильный додекаэдр объемом 64 + 32 ϕ (и длиной ребра 4 ϕ — 4).

Таким образом, разница в объеме между окружающим правильным додекаэдром и замкнутым кубом всегда равна половине объема куба, умноженного на ϕ .

Из этих соотношений выводятся простые формулы для объема правильного додекаэдра с длиной ребра a через золотую середину:

V = ( aϕ ) 3 ·14(5 + √ 5 )

V =14(14 ϕ + 8) а 3

Отношение к золотому прямоугольнику

Золотые прямоугольники отношения ( ϕ + 1): 1 и ϕ : 1 также идеально вписываются в правильный додекаэдр. Пропорционально этому золотому прямоугольнику край замкнутого куба равен ϕ , когда большая длина прямоугольника равна ϕ + 1 (или ϕ 2 ), а короткая длина равна 1 (ребро, общее с правильным додекаэдром).

Кроме того, в центре каждой грани правильного додекаэдра образуют три пересекающихся золотых прямоугольника.

Связь с 6-кубом и ромбическим триаконтаэдром

Проекция 6-полукуба на правильную додекаэдрическую огибающую

Его можно спроецировать в 3D из 6-мерного 6-полукуба, используя те же базисные векторы, которые образуют оболочку из 6-куба . Показанные здесь 12 внутренних вершин, которые не соединены ребрами внешней оболочки с 6D нормальной длиной √ 2 , образуют правильный икосаэдр .

Используемые базисные векторы трехмерной проекции [ u , v , w ]:

u = (1, ϕ , 0, −1, ϕ , 0)

v = ( ϕ , 0, 1, ϕ , 0, −1)

w = (0, 1, ϕ , 0, −1, ϕ )

Другие додекаэдры

Существует 6 384 634 топологически различных выпуклых додекаэдра, исключая зеркальные изображения — число вершин колеблется от 8 до 20. (Два многогранника «топологически различны», если они имеют внутренне различное расположение граней и вершин, так что их невозможно исказить в другой, просто изменяя длину кромок или углы между кромками или гранями.)

Топологически различные додекаэдры (исключая пятиугольные и ромбические формы)

Равномерные многогранники:
- Десятиугольная призма — 10 квадратов, 2 декагона, симметрия D _10h , порядок 40.
- Пятиугольная антипризма — 10 равносторонних треугольников, 2 пятиугольника, симметрия D _5d , порядок 20
Твердые тела Джонсона (со стандартной поверхностью):
- Пятиугольный купол — 5 треугольников, 5 квадратов, 1 пятиугольник, 1 декагон, симметрия C _5v , порядок 10
- Курносый дисфеноид — 12 треугольников, D _2d , порядка 8
- Удлиненная квадратная дипирамида — 8 треугольников и 4 квадрата, симметрия D _4h , порядок 16
- Метабидоуменьшенный икосаэдр — 10 треугольников и 2 пятиугольника, симметрия C _2v , порядок 4
Конгруэнтное неправильное лицо : ( переходное лицо )
- Гексагональная бипирамида — 12 равнобедренных треугольников , двойная шестиугольной призме , симметрия D _6h , порядок 24
- Шестиугольный трапецоэдр — 12 воздушных змеев , двойных шестиугольной антипризме , симметрия D _6d , порядок 24
- Тетраэдр Триаки — 12 равнобедренных треугольников, двойственный усеченному тетраэдру , симметрия T _d , порядок 24
Другое менее регулярное столкновение:
- Гендекагональная пирамида — 11 равнобедренных треугольников и 1 правильный пятиугольник , C _11v , порядок 11
- Трапецо-ромбический додекаэдр — 6 ромбов, 6 трапеций — двойственный треугольному ортобикуполу , симметрия D _3h , порядок 12
- Ромбо-шестиугольный додекаэдр или удлиненный додекаэдр — 8 ромбов и 4 равносторонних шестиугольника , симметрия D _4h , порядок 16
- Усеченный пятиугольный трапецоэдр , D _5d , порядок 20, топологически эквивалентен правильному додекаэдру

Интересные факты о додекаэдре

Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.

Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.

Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.

Игрушки древних римлян

На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.

Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.

В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.

Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.

Что такое тетраэдр

С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги. Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью. В фигуре есть также четыре вершины и шесть ребер.

Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.

На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:

мостов;
перекрытий;
балок;
ферм;
пролетов зданий.

Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.

Делаем двадцатигранник

Икосаэдр состоит из одинаковых по размеру равнобедренных треугольников. Его можно легко сложить, используя представленную на рисунке 2 развертку. Возьмите прямоугольный лист бумаги. Начертите на нем двадцать одинаковых по размеру и форме треугольников, расположив их в четырех рядах. При этом каждая грань одного будет одновременно являться стороной другого. Полученный шаблон используйте для изготовления заготовки. Она будет отличаться от основы-развертки наличием припусков для склеивания по всем внешним линиям. Вырезав из бумаги заготовку, согните ее по линиям. Формируя из бумаги многогранник, замыкайте крайние ряды между собой. При этом вершины треугольников соединятся в одну точку.