Тайна египетского треугольника, история появления, строительные советы фото zdorpoc.ru

Содержание

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

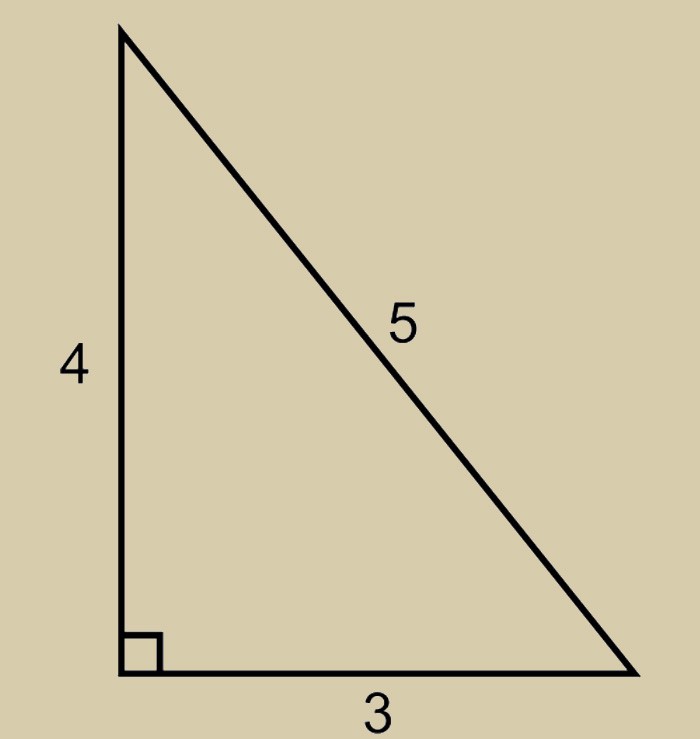
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

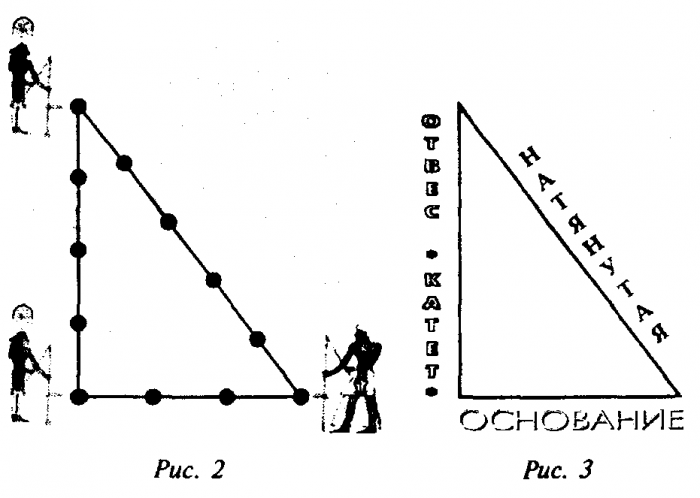
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

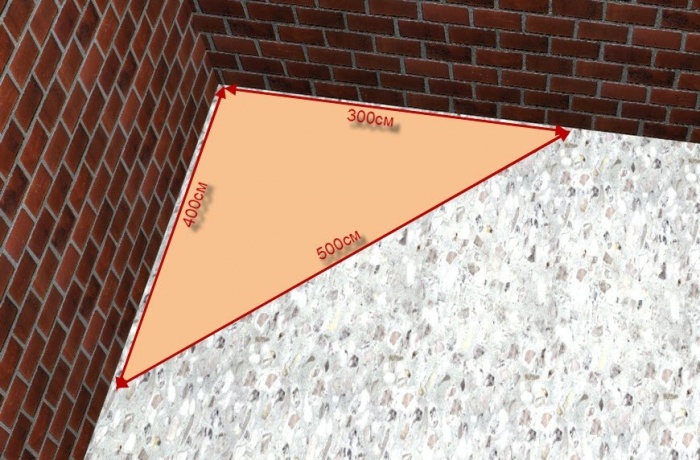
Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Отношение самой длинной стороны этого треугольника к самой короткой стороне – «два к одному». То есть самая длинная сторона в два раза длиннее самой короткой стороны. Она также изготовлена из пластика и широко используется в дизайне, рисовании и Строительных приложений.

Вы можете найти бесконечное количество примеров правильных треугольников. Один из самых известных – «Треугольник 3, 4, 5». Египтяне использовали этот треугольник для съемки земли. Некоторые считают, что они также использовали его для разработки своих пирамид. Плотники и деревообработчики также используют его, чтобы сделать их углы квадратными. Он доказал, что для правого треугольника сумма квадратов двух сторон, которые соединяются под прямым углом, равна квадрату третьей стороны. Третья сторона – сторона, противоположная правому углу, называется гипотенузой правого треугольника.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Две более короткие стороны обычно называются «ногами». Эта формула называется Пифагорейской теоремой в честь Пифагора. Мы можем проверить, что теорема Пифагора верна, подставляя значения. Квадратный корень из 169 равен 13, которая является мерой гипотенузы в этом треугольнике. Теорема Пифагора имеет много применений. Вы можете использовать его, чтобы проверить, является ли треугольник правильным треугольником. Или вы можете использовать его, чтобы найти недостающие меры сторон.

Подставьте значения в формулу и выполните вычисления, как это. Джимми Данн пишет как Алан Уинстон. До того, как произошла физическая ориентация и расположение новой пирамиды, необходимо было провести значительное планирование под руководством «королевского мастера-строителя». В конечном итоге ответственность возлагалась на визиря, который, как правило, возглавлял все королевские работы. Первым шагом в этом процессе стали специалисты, которые разработали планы пирамиды на папирусе. После начала строительства планы и эскизы были сделаны на папирусах или плоских плитах из известняка.

Как треугольник используется в строительстве?

Треугольник используется в строительстве, чтобы убедиться, что что-то квадратное или что-то квадратное. Квадрат скорости представляет собой небольшой треугольный инструмент, используемый для обозначения углов стропила. Один из методов проверки квадрата комнаты или одной стены, перпендикулярной другой, состоит в том, чтобы измерить 3 фута вдоль одной стены и сделать отметку карандашом, чтобы они измеряли 4 фута вдоль другой стены и делали метку карандаша. Затем измерьте диагонально от метки карандаша до метки карандаша. Если число составляет 5 футов, две стены квадратные друг к другу.

Разметка под фундамент своими руками

Качество постройки в огромной степени зависит от того, насколько правильно была выполнена разметка под фундамент

Занимаясь этой работой важно с максимальной точностью выдержать все прямые углы. Разметка фундамента своими руками под частный дом может быть выполнена несколькими способами. Чаще всего используются метод «египетского» треугольника и метод двух кривых

Поэтому в этой статье рассмотрим именно их

Чаще всего используются метод «египетского» треугольника и метод двух кривых. Поэтому в этой статье рассмотрим именно их.

Какие инструменты понадобятся?

Производится разметка фундамента своими руками с применением инструментов:

Рулетки;
Шнура;
Гидроуровня и отвеса;
Помимо этого понадобятся деревянные колышки.

С чего начать разметку?

Итак, как провести разметку фундамента? Для начала следует определить две исходные точки, вбив колышки по углам будущего здания, находящимся на одной прямой со стороны его самой длинной стены. Далее от них нужно будет провести перпендикуляры, таким образом отметив внешний контур смежных стен.

«Египетский треугольник». Самый простой метод

Разметка фундамента своими руками быстрее всего может быть произведена методом «золотого» треугольника, имеющего соотношение длин сторон 5*3*4. Мероприятие при этом выполняется в несколько этапов:

1. Для начала нужно найти длинную веревку и завязать на ней четыре узла. Первый – на конце, второй на расстоянии 3м, третий в четырех метрах от второго и последний в пяти метрах от третьего; 2. После этого самый первый и самый последний узлы соединяют гвоздем. По гвоздю следует вбить и в каждый из промежуточных узлов; 3. При этом длинную сторону получившегося треугольника нужно расположить вдоль линии между двумя уже вбитыми колышками; 4. Вдоль короткой стороны проводят требуемый перпендикуляр; 5. На полученной прямой, вбивают третий колышек на расстоянии равном ширине здания.

Важно: Правильность всех замеров следует обязательно проверить. Для этого между вбитыми кольями по диагоналям натягивают два шнура и связывают в месте пересечения

Paste a VALID AdSense code in Ads Elite Plugin options before activating it.

Метод двух дуг

Разметка фундамента своими силами этим методом выполняется также с использованием веревки. Предварительно от одного из колышков в обе стороны по уже имеющейся прямой отмеряют равные расстояния и отмечают найденные места. Далее к одной из полученных точек прикрепляют веревку с привязанным на противоположном конце гвоздем. Натянув ее проводят дугу напротив того колышка, от которого отмерялись расстояния. Затем веревку крепят ко второму отмеченному месту и чертят еще одну дугу. Из той точки, где дуги пересекутся, проводят линию к колышку. В результате получается прямой угол между ней и уже имеющейся линией.

На заключительном этапе к кольям на высоте будущего фундамента привязывают шнур, поверяя горизонтальность его положения со всех четырех сторон, пользуясь строительным уровнем. Для ленточного фундамента чертят внутренний контур параллельно найденному внешнему и также натягивают шнур.

Совет: В том случае, если траншею предполагается копать с привлечением техники, шнуры лучше не использовать. В процессе работы они могут порваться. Линии между найденными точками в этом случае стоит прочертить песком. Для нахождения центров столбов столбчатого фундамента, от найденных углов вдоль прочерченных линий отмеряют необходимые расстояния и ставят отметки. Далее проверяют прямоугольность углов, получившихся на пересечении линий (соединяющей полученные точки на противоположных сторонах и линии периметра, на которой расположены отметки).

Разметка фундамента своими руками, как можно было заметить – процедура не такая уж и сложная. Самое главное, делать все аккуратно, хорошо натягивать веревку и обязательно проверять полученный результат методом диагоналей.

Другие способы доказательства теоремы

Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.

Методом площадей

Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:

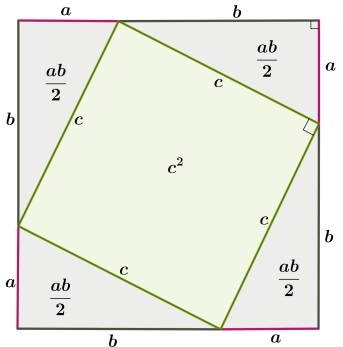
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.

Площадь внешнего квадрата включает в себя:

сумму площадей четырех прямоугольных треугольников;
площадь внутреннего квадрата.

Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.

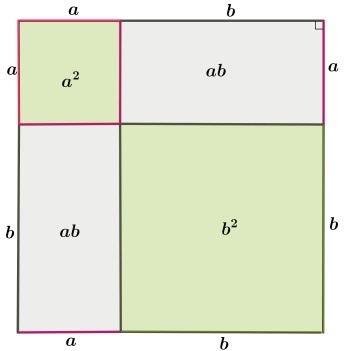
Значит:

4ab2=2ab ⇒ c2=a2+b2, что и нужно было доказать.

Методом бесконечных малых

Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.

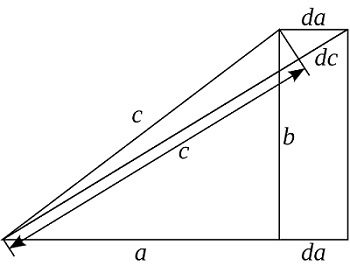
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем

da/ca = c/a, b = const

Разделяя переменные составляется дифференциальное уравнение:

c x dc = a x da

Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:

c2 = a2 + const

определяя из начальных условий константу интегрирования, получим:

a = 0 ⇒ c2 = b2 = const

Таким образом мы определяем, что

c2 = a2 + b2

Теорема доказана!

Какие существуют альтернативные варианты

Как создать прямой угол

Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.

В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.

Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.

Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.

Как создать другие углы?

Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.

Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол. Края должны быть соединены

Края должны быть соединены.

Получить 60 градусов можно с применением двух треугольников по 30 градусов. Чаще всего используются для создания декоративных элементов.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна
квадрату длины гипотенузы. В виде формулы записывается это так:

a²+b²=c²

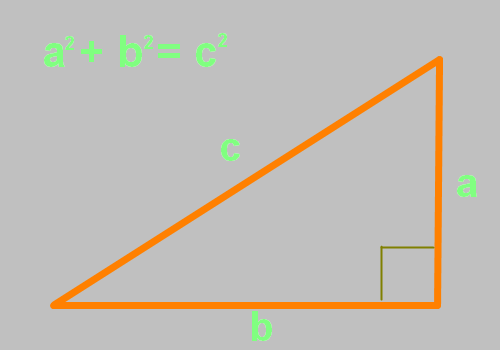
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем
размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник»

Это треугольник со сторонами 3, 4 и 5,
причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов

Проверим
данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все
сходится!

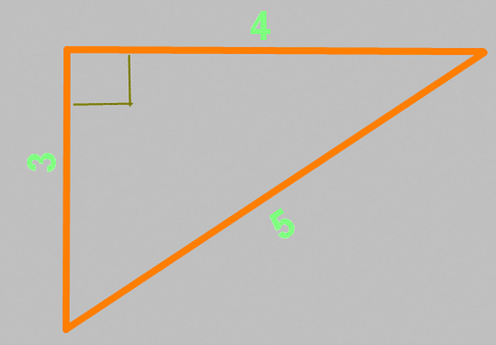
А теперь применим теорему на практике.

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

все стороны и площадь состоят из целых чисел, как говорилось выше;
согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

Что такое Египетский треугольник на стройке? В чем его особенность +Фото и Видео

Строительство с применением египетского треугольника древний способ, активно используемый до сих пор современными строителями. Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.

Но, скорее всего, свойства уникальной фигуры не были оценены в те времена, пока не появился Пифагор, сумевший проанализировать и оценить изящные формы фигуры.

Египетский треугольник известен еще с древних времен. Он был и остается популярен в строительстве и архитектуре много веков.

Считается, что создал геометрическую конструкцию великий греческий математик Пифагор Самосский. Благодаря ему сегодня мы можем использовать все свойства геометрической постройки в области строения.

Заключительное слово

Что бы ни говорили противники описанного метода измерений, но «египетский треугольник» в значительной степени помогает строителям в выведении прямых углов. Конечно, при условии его правильного использования. Тем более что навязать 12 узлов на верёвке на определённом расстоянии один от другого много времени не потребует. Также это не потребует и финансовых затрат, связанных с наймом геодезиста с необходимым оборудованием.

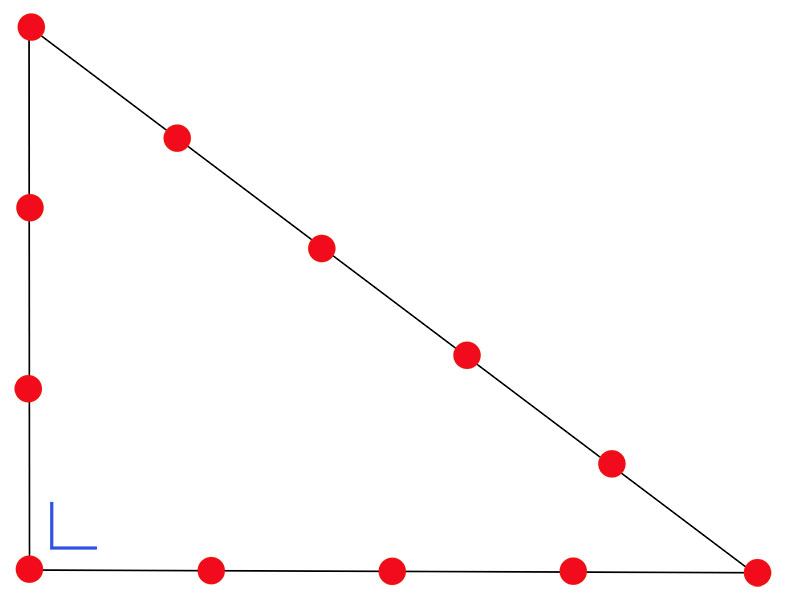ФОТО: profipol.dp.uaТак должны быть расположены узлы на верёвке для построения «египетского треугольника»

Watch this video on YouTube

Предыдущая DIY HomiusПрочные хомуты из ПЭТ-бутылки за минуту Следующая DIY HomiusСмеяться или плакать: ошибки во время ремонта

Египетский треугольник в строительстве

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Стороны конструкции имеют следующее соотношение друг к другу:

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять

В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам

Альтернативные способы построить прямой угол на 90 градусов

Как получить египетский треугольник при помощи верёвки

Как построить угол в 45, 30 и 60 градусов

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть

Края должны совпасть.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках

Египетский треугольник

Организация: МБОУ «Кудеихинская СОШ»

Населенный пункт: Чувашия,Порецкий район, с. Кудеиха

«Египетский треугольник» — небольшая тема в курсе геометрии 8 класса

Очень важно, чтобы материал, с которым учащиеся познакомятся на этом уроке, вызвал у них желание учиться

Урок начинается с практической работы: несколько учеников на доске (а остальные в тетрадях) строят треугольник по трём сторонам, если стороны равны: а) 3, 4, 5; б) 6,8,10; в) 5,12,13 (при этом не обязательно указывать единицы измерения). Затем ребята получают задание – измерить больший угол этих треугольников. Ответы оказываются близки к 90°. Тогда учитель говорит: «Посмотрите, ребята! Треугольники у всех расположены по-разному, длины сторон разные, а результаты у всех получились примерно одинаковыми. Чем объясняются небольшие различия в данных? Тем ли, что здесь нет никакой закономерности, или тем, что закономерность есть, но нашими инструментами мы не можем установить её с достаточной точностью?» Учащиеся склоняются к тому, что если все углы получились близкими к прямым, то, значит, какая-то закономерность существует. «Как же мы сформулируем утверждение, которое будем доказывать?» — спрашивает учитель. Класс постепенно находит нужную формулировку.

«Если треугольник имеет стороны а, в, с и а² + в² = с², то угол, противолежащей стороне с прямой». Это доказательство разбирается в учебнике А.В.Погорелова, задача №17. Далее разбирается теорема Пифагора.

Затем предлагается устная работа: не выполняя предложенных заданий, определить, когда необходимо воспользоваться теоремой Пифагора, а когда – обратной к ней.

Задания

В прямоугольном треугольнике гипотенуза и катет соответственно 13 и 5. Найдите второй катет.
В прямоугольном треугольнике катеты равны 1,5 и Найдите гипотенузу.
Определите вид треугольника, стороны которого равны 6, 8 и 10.

Далее учащиеся выполняют практическую работу: на тонкой верёвке делаются метки, делящие её на 12 равных частей, связывают концы, а затем растягивают верёвку в виде треугольника со сторонами 3,4 и 5. тогда угол между сторонами 3 и 4 оказывается прямым. Делается вывод: если стороны треугольника пропорциональны числам 3.4 и 5, то этот треугольник прямоугольный.

Этот факт использовался египтянами для построения на местности прямых углов.

3² + 4² = 5², говоря иначе, числа 3,4 и 5 корни уравнения х² + у² = z². Поэтому треугольник со сторонами 3,4 и 5 единиц называют египетским.

Сразу же возникает вопрос: нет ли у этого уравнения целочисленных решений? Прямоугольными являются также треугольники со сторонами 5,12,13; 8,15,17; 7,24,25, что соответствует теореме, обратной к теореме Пифагора: 13² = 5² + 12²; 17² = 15² + 8²;

25² = 24² + 7².

Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками. В конце урока уместно прочитать наиболее известные стихи, посвящённые тереме Пифагора.

Теорема Пифагора

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдём;

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путём

К результату мы придём.И.Дырченко

Литература.

Шустер Ф.М.Материал для внеклассной работы по математике ( Минск: Народная света. 1984)
Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа.- М.: Просвещение, 1996.
Погорелов А.В. Геометрия. 7-9 классы –М.: Просвещение, 2013.

Приложения:

file0.docx.. 16,2 КБ

Опубликовано: 22.10.2020

Прямой угол при строительстве. Нужна лишь веревка и помощь египтян.

При любой стройке часто сталкиваешься с проблемой разметки прямого угла на местности. Несомненно, что существуют всевозможные лазерные приборы, которые эту проблему решают на раз два. Они удобны и практичны. Но имеют один существенный недостаток — цена. Если вы профессионал — тогда — да, этот прибор незаменим. Ну а если любитель, и нужно всего пару раз построить прямой угол, то лишние расходы не к чему. Всегда можно обойтись веревкой, как делали с незапамятных времен. Даже египетские пирамиды строили с помощью этого способа и это до сих пор не потеряло актуальности.

Есть метод, который вполне рабочий и основан он на школьной геометрии. Допустим вам нужно поставить, грубо говоря, столбы под прямым углом друг к другу(угол забора). Этот способ я применял, когда делал на своем участке стол и вбивал трубы в землю. Конечно можно было и на глаз, но так как с этим у меня всегда была беда, то воспользовался обычной веревкой. Главное в этом, чтоб она не растягивалась, вот и все. У меня под рукой оказался мягкий тонкий провод, что вполне подходило под эти задачи.

Суть основывается на, так называемых, египетских треугольниках. Их еще называют Героновыми, Евклидовыми, Пифагоровыми. Не будем вдаваться в подробности, отмечу лишь, что зачастую египетские — это частное от всех остальных. Лишь Пифагоровы тройки точно отвечают нашим требованиям.

Вот этот замечательный треугольник. Его стороны являются целым числом, что нам и нужно. Соответственно. Берем веревку и строим с помощью нее эту фигуру на земле. И не обязательно откладывать именно 3 метра, 4 и 5. Самое главное — соблюсти пропорции. За единицу измерения можно взять и полметра, а можно и любую другую удобную длину. Для примера — полуметровые соотношения — 1,5 м 2 м и 2,5 м. Просто, чем больше размеры — тем точнее наши построения.

Итак. Забиваем столб, от которого нам и надо построить прямой угол. От него отмечаем 3 метра и забиваем колышек на этом месте. К колышку привязываем веревку в пять метров а к столбу — четырехметровую. Связываем свободные концы друг с другом и натягиваем веревки, чтобы обе ни где не провисали. Когда найдем это место — туда колышек и все. Построения закончены — прямой угол у нас имеется. А дальше по линиям веревки забиваем столбы на нужном нам расстоянии.

Просто, дешево, быстро. Главное в этом деле — не спешить, и чем больше точность в отрезках веревки — тем ближе угол к 90 градусам.

Кстати, есть еще пару методов на основе треугольников и знаний геометрии, но об этом как нибудь в следующий раз. А на этом пока все.

Тайна египетского треугольника, история появления, строительные советы фото

Египетский треугольник в строительстве

Альтернативные способы построить прямой угол на 90 градусов

Как получить египетский треугольник при помощи верёвки

Как построить угол в 45, 30 и 60 градусов

История египетского треугольника

Как треугольник используется в строительстве?

Разметка под фундамент своими руками

Какие инструменты понадобятся?

С чего начать разметку?

Paste a VALID AdSense code in Ads Elite Plugin options before activating it.

Другие способы доказательства теоремы

Методом площадей

Методом бесконечных малых

Какие существуют альтернативные варианты

Как создать прямой угол

Как создать другие углы?

Теорема Пифагора

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Из истории

Строение

Обратное доказательство

Особенности

Небольшие хитрости

Что такое Египетский треугольник на стройке? В чем его особенность +Фото и Видео

Заключительное слово

Египетский треугольник в строительстве

Альтернативные способы построить прямой угол на 90 градусов

Как получить египетский треугольник при помощи верёвки

Как построить угол в 45, 30 и 60 градусов

Египетский треугольник

Опубликовано: 22.10.2020

Прямой угол при строительстве. Нужна лишь веревка и помощь египтян.

Похожие записи: