Содержание
Электронный игральный кубик
Чем ближе друзья живут, тем их сложнее собрать. В ход идёт куча предлогов — передвинуть мебель на даче, починить машину в гаражно-оздоровительном комплексе. Порубиться в тихие настольные игры — «Манчкин» или ещё какую-нибудь «Цивилизацию». И вот, момент настал, пенные напитки в холодильнике, все собрались и вдруг выясняется, кто-то потерял игральные кубики. Если кубики обычные, шестигранные, их можно поискать у младшего брата. Но как быть с четырёх-, двенадцати- или двадцатигранными? Подземелья так и останутся неисследованными, а драконы — непобеждёнными.

Наши универсальные электронные кости работают в режиме эмуляции стандартных кубиков d4, d6, d12 и d20. Режим работы задаётся потенциометром и выводятся на левую LED-матрицу. Чтобы запустить генератор случайных чисел, возьмите гаджет в руки и встряхните его. Гироскоп запустит генератор случайных чисел и результат «броска» появится на правой матрице. Для четырёх- и шестигранных кубиков значение выводится крупными точками, как на настоящих костях, для остальных кубиков используется цифровая индикация.
Томограф Siemens go.Now
Мультиспиральный томограф Центра КТ «Ами» — это аппарат нового поколения Siemens go.Now, который дает оптимальное качество КТ-снимков при значительно сниженной лучевой нагрузке. На полученных томограммах анатомические структуры визуализируются с высокой точностью. Такой результат обеспечивают новые технологии, использованные в нашем аппарате.
Томограф Siemens go.Now дает распределенную лучевую нагрузку, адаптированную для каждого пациента и каждого отдельного исследования. Например, технология снижения лучевой нагрузки для определенных частей тела при сканировании головы защищает хрусталики глаз, при сканировании грудного отдела — грудную клетку.
Технология «Оловянный фильтр» повышает качество изображения мягких тканей и костных структур.
Технология низковольтного сканирования позволяет повысить диагностическую уверенность, увеличив четкость изображения. При этом значительно уменьшается количество контрастного вещества, что делает исследование безопасней и дешевле.
Технология «Оловянный фильтр» повышает качество изображения мягких тканей и костных структур.
Технология низковольтного сканирования позволяет повысить диагностическую уверенность, увеличив четкость изображения. При этом значительно уменьшается количество контрастного вещества, что делает исследование безопасней и дешевле.
New World of Darkness
в WoD кидается Xd10, и считается количество костей на которых выпало 8 или больше. Кости на которых выпало 10 учитываются в успех и кидаются ещё раз, и учитываются так же как и первые брошенные кости, если опять выпадает 10, то процесс повторяется. Т.е. возможно да же на 1d10 выкинуть бесконечное значение успехов, правда вероятность этого очень низкая. Как оказалось, график плотностей вероятности данного вида бросков лучше всего отображается используя логарифмическую шкалу. Для тех кто не знает: на логарифмической шкале одно деление означает увеличение/уменьшение значения в 10 раз, на два деления — в 100 раз и т.д.
По графику видно что при такой системе подсчёта результатов при броске Xd10 вероятности 0..(X-1) успеха достаточно велики. Вероятность выпадения X и больше падает во много раз с каждым новым успехом.
Такие броски хорошо описывают процессы где вероятность определённых значений отличаются не сильно, но уменьшается с ростом величины. При этом несмотря на наличие границы, есть очень маленькая вероятность получить и большие значения. Такое распределение неплохо подходит для событий имеющих какие-то ограничения, которые при этом всё же изредка могут быть преодолены
2d6
Проанализируем плотность вероятностей для 2d6. Для этого нам потребуется составить матрицу, столбцы которой будут результатами первого броска, а строки — второго.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
Теперь нам нужно высчитать вероятности всех возможных исходов при двух бросках и записать их в ячейки матрицы. Если вероятность выбросить на d6 1 равна 1/6, то вероятность получить 1 и во втором броске равна 1/6 от 1/6, то есть 1/36 или 2,78%.
Таким образом в каждой ячейке такой матрицы получаем значение 2,78%
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 2 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 3 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 4 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 5 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 6 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
Однако если мы заполним ту же самую матрицу значениями, которые получаются в сумме двух бросков, то получим:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Из таблицы видно, что к значению 2 от броска 2d6 ведет только 1 исход, когда оба броска показали 1. В то время как получить 4 можно одним из трех исходов: 3 и 1, 2 и 2, 1 и 3. Выходит, что вероятность получить 4 при броске 2d6 равна сумме вероятностей 3 исходов, вероятность каждого из которых равна 2,78%. Получаем 2,78%+2,78%+2,78%=8,33% (помним про округление процентов).
Если составить таблицу вероятности для всех значений, получим:
| Значение | Вероятность |
|---|---|
| 2 | 2,78% |
| 3 | 5,56% |
| 4 | 8,33% |
| 5 | 11,11% |
| 6 | 13,89% |
| 7 | 16,67% |
| 8 | 13,89% |
| 9 | 11,11% |
| 10 | 8,33% |
| 11 | 5,56% |
| 12 | 2,78% |
В графическом представлении это выглядит так:
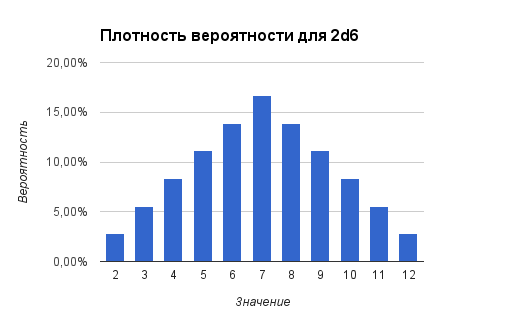
Заметим, что при учете двух бросков мы получаем распределение Гаусса (оно же нормальное распределение). Вероятность получить в результате двух бросков срединное значение (в нашем случае это 7) значительно выше, чем вероятность получить крайние значения (2 или 12). Соответственно гораздо чаще результаты бросков для 2d6 будут находится среди значений 5-9 и редко показывать 2-4 или 10-12. В некоторых случаях от случайной величины требуется именно такое поведение.
Кривые вероятности выбросить значение X+ или X- так же будут иметь нелинейный вид:
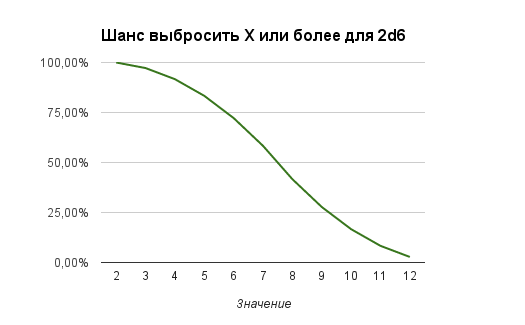
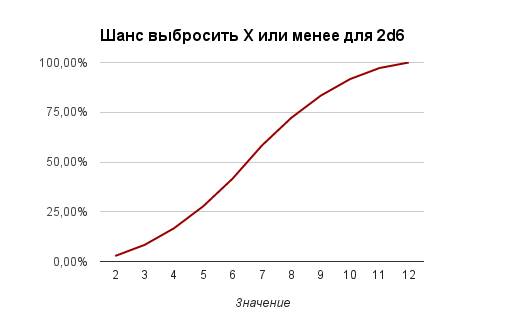
Если представить полученные данные в табличной форме, то:
| Значение | Вероятность | Значение | Вероятность | Значение | Вероятность |
|---|---|---|---|---|---|
| 2 | 2,78% | 2+ | 100,00% | 2 | 2,78% |
| 3 | 5,56% | 3+ | 97,22% | 3- | 8,33% |
| 4 | 8,33% | 4+ | 91,67% | 4- | 16,67% |
| 5 | 11,11% | 5+ | 83,33% | 5- | 27,78% |
| 6 | 13,89% | 6+ | 72,22% | 6- | 41,67% |
| 7 | 16,67% | 7+ | 58,33% | 7- | 58,33% |
| 8 | 13,89% | 8+ | 41,67% | 8- | 72,22% |
| 9 | 11,11% | 9+ | 27,78% | 9- | 83,33% |
| 10 | 8,33% | 10+ | 16,67% | 10- | 91,67% |
| 11 | 5,56% | 11+ | 8,33% | 11- | 97,22% |
| 12 | 2,78% | 12 | 2,78% | 12- | 100,00% |
Получается, что если мы хотим получить генератор случайных чисел, который выдает распределение близкое к тому, что встречается «в природе», то использование пары кубиков или учет двух бросков дает нам эту возможность.
Ровно как и запись 2d6 имеет преимущество над 2-12 как раз в том, что указывает не только на диапазон, но и на плотность вероятностей.
Если же нам требуется получить нормальное распределение в промежутке от 0 до 10, то с помощью дайсов это можно организовать как бросок 2d6 из результата которого будем вычитать 2. Вспоминая описанные ранее обозначения, это 2d6-2.
Если такая перемена в графике произошла когда мы добавили второй бросок, то что произойдет, если ввести третий?
Как, кидая кубик, получить любую вероятность?
В школе я увлекался настольными играми, в основном варгеймами. Придумывал правила, изготавливал поля, юниты и проводил с друзьями увлекательные баталии. Однако вскоре для моделирования различных игровых ситуаций перестало хватать стандартного игрового кубика, с помощью которого можно получать вероятности, кратные одной шестой. Поиск решения породил пару интересных математических задач, связанных с теорией вероятности.
Итак, допустим, имея игровой кубик, нам нужно получить событие, вероятность которого равна 1/5. Для этого рассмотрим такой процесс: кубик бросается до тех пор, пока на нём не выпадет число, не равное шести. Очевидно, что в конечном итоге вероятности получить одно из чисел от 1 до 5 будут равны 1/5. Найдём, какое в среднем количество бросков потребуется сделать, чтобы серия шестёрок завершилась другим числом (иными словами, математическое ожидание данное величины).
С вероятностью
Её несложно будет вычислить, представив в следующем виде:
В итоге математическое ожидание количества бросков для получения результата равно 1,2.
Рассмотрим теперь, как получать события с вероятностями, меньшими 1/6. К примеру, как сделать механический генератор случайных чисел от 1 до 36. Для этого можно обратиться к помощи систем счисления. Тридцать шесть чисел от 0 до 35, записанные в шестеричной системе счисления будут двузначными, от 00 до 55. Таким образом, если взять два кубика, таких, чтобы по виду можно было определить, какой из них первый, а какой второй, и нанести им на грани цифры от 0 до 5, каждый бросок будет нам давать случайное число от 0 до 35, записанное в шестеричной системе. Чтобы исключить необходимость оперирования недесятичной системой и получать числа из диапазона 1..36, нанесём на один кубик числа 1, 2, 3, 4, 5, 6, а на другой – 0, 6, 12, 18, 24, 30.
Если же нам необходимы случайные числа от 1 до 18, то на первый кубик наносятся числа от 1 до 6, а на второй: 0, 0, 6, 6, 12, 12.
Объединив оба подхода, можно с помощью трёх кубиков получать события с вероятностями, кратными 1/100. Для этого возьмём 3 кубика, два, такие, как в системе, дающей числа от 1 до 36, а на грани третьего нанесём числа 0, 0, 36, 36, 72, 72. С её помощью будем получать числа от 1 до 108. Если теперь при выпадении значений от 101 до 108 бросать кубики снова, и останавливаться только в случае получения числа от 1 до 100, мы сможем замоделировать любую вероятность, кратную целому числу процентов. Даже для самых сложных правил настольных игр этого должно хватить.
По мотивам этой темы можно составить задачу. Имеется арифметическая прогрессия a 1 , a 2 , a 3 , … с разностью d, и геометрическая прогрессия b 1 , b 2 , b 3 , … со знаменателем -1 1 b 1 +a 2 b 2 +a 3 b 3 +…. Разобравшись с тем, как мы находили математическое ожидание количества бросков, её решить будет несложно.
Поздравляю Вас с наступающим Новы Годом и желаю, чтобы все возможные расклады были для Вас удачными!
Источник
Современное применение
Сейчас стандартные кубики представляют собой все ту же конструкцию, что применялась ранее. Однако для использования в казино был необходим определённый стандарт, который бы исключал махинации. Поэтому было принято решение унифицировать все малые и большие игральные кости и принять лишь те, грань которых составляет 16 миллиметров в поперечнике. В то же время в результате проверок вероятности возникновения некоторых комбинаций выяснили, что при высверливании точек на поверхности кубика смещается его центр тяжести. Поэтому современные игральные кости маркируют цветом, что не ведёт к образованию искажений в функционировании источника случайностей. Также были утверждены методы маркирования граней кубика, общая сумма трёх сторон какого всегда равна 7. При нанесении цифровых отметок от 1 до 3 по часовой стрелке относительно угла эти фишки называются правыми, если наоборот — левыми.
Dungeons & Dragons
Большинство проверок сводится к «выбросить на 1d20 больше чем DC-skill» или к аналогичным. Для данной простой проверки даже графики-то не нужны, всё можно посчитать в уме. Вероятность выкинуть 10 или больше: 1/20*11 = 55%. Вероятность выкинуть 15 или больше: 6/20 = 30%
немного сложнее с новой системой Advantage/Disadvantage, когда бросается 2d20, и берется лучшее/худшее значение: min(2d20) и max(2d20). Вот графики для них:
- При наличии advantage вероятность выбросить 20 — почти 10%! Аналогичная вероятность выкинуть 1 при disadvantage. Плотности вероятности обоих вариантов являются зеркальными отображениями друг-друга, поэтому свойства одной «зеркально» являются свойствами другой.
- Математическое ожидание смещается на 3.3 вправо или влево. Однако распределение не Гауссово, и даже не похоже на изначальное, так-что это не эквивалентно бонусу/штрафу 3.3
- при advantage вероятность получить 9 или меньше 20%, в то время как на обычном 1d20 —45%
Броски 2dN с выбором лучшего/худшего хороши для процессов вида «чем больше, тем вероятнее» или «чем меньше тем вероятнее», например при случайном выборе «силы» для воина, или при выборе количества трезвенников в баре, количество проституток в церкви, количество честных людей в правительстве, средняя школьная оценка мелкого воришки, вероятность что кошка приземлится на ноги. Так же эти броски хороши для описания процессов которые следуют закону Мерфи, например вероятность что бутерброд упадёт маслом вниз.
Хоббиты
Везучие хоббиты могут перекидывать кубик, если на нём выпало значение 1. Если вам интересно как это влияет на вероятности выбросить то или иное значение, то можете изучить следующие графики
Тут всё просто: вероятность получить 1 — 1/5
При наличии преимущества, вероятность получить 1 у халфлинга меньше одной тысячной процента, а остальное видно на графике
Особые дайсы[]
Дайсы с особыми символами для WFRP 3
Некоторые игры используют специальные дайсы, которые сложно достать в обычных магазинах. Например, система FUDGE и её потомки (в частности, FATE) используют Fudge dice — шестигранники с гранями +1, +1, 0, 0, −1, −1. Основной бросок 4dF даёт число от −4 до +4, причём результаты −1, 0 и +1 наиболее вероятны. Другой пример — кости с особыми символами, применяемые, к примеру, в третьей редакции Warhammer Fantasy Roleplay («кость характеристик», «кость удачи» и так далее).
Некоторые системы используют «белые кубики», на грани которых наносятся символы в зависимости от нужд игры. Набор таких кубиков становится частью характеристик персонажа. На этом принципе основаны системы Bones и The World, the Flesh, and the Devil.
Иногда особые дайсы можно сымитировать с помощью обычных. Если в распоряжении группы есть кубик с нужным числом граней, можно расписать таблицу соответствий его значений нужным. Например, фудж-дайсы часто имитируются обычными шестигранниками, на которых 1 и 2 считается за −1; 3 и 4 за 0; 5 и 6 за +1. Ещё один способ сымитировать необычный кубик — наклейки на грани или цветовая маркировка фломастером. Иногда можно сымитировать и кубик с необычным числом граней, например, отбрасывая несоответствующие значения (кидать d7 как d8 с перебросом восьмёрок).
Шаг первый. Подключаем индикатор
Семисегментный индикатор — это восемь светодиодов, собранных в одном корпусе. Семь из них служат для отображения цифр, некоторых букв и знаков. Восьмой — выводит точку в правом нижнем углу дисплея.
У индикатора десять ножек: по пять сверху и снизу. Центральные ножки в каждой группе — это общий минус. Достаточно подключить только одну из них. Оставшиеся восемь — плюсы отдельных сегментов индикатора. Если подать на такую ножку ток, сегмент загорится.
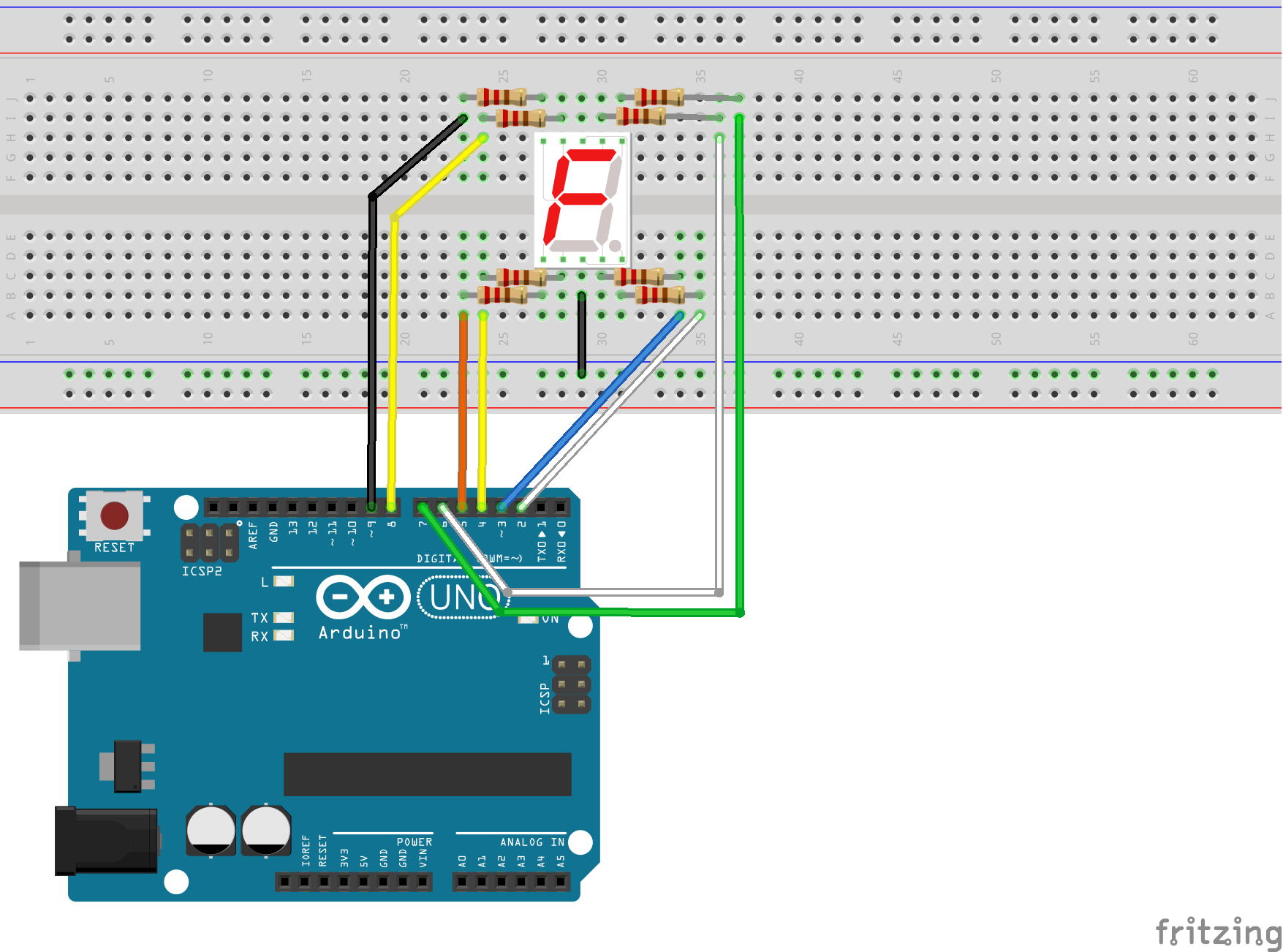
Установлю индикатор в самом центре макетной платы. Затем подключу одну из средних ножек к общему минусу, а плюсовые ножки к контактам платы Arduino, начав с контакта номер 2.

Проводов много, легко ошибиться. Поэтому проверю подключение индикатора с помощью простой программы. Она по очереди включит все сегменты.
Микроконтроллер включает первый сегмент на самом маленьком по номеру контакте, ждёт секунду и переходит к следующему. Я сделал это с помощью циклов, о которых рассказывал в статье о сборке электронного метронома. Не буду на этом ещё раз останавливаться, благо впереди ещё много сложных вопросов.

Обратите внимание, в цикле я только включаю сегменты, но не выключаю их. Светодиоды гаснут только после перезагрузки платы
Если нажать кнопку RESET (в переводе с английского это означает сброс) — плата перезагрузится и светодиоды погаснут, а потом начнут зажигаться по новой. Это происходит потому, что Arduino не подаёт ток на контакты, если в программе нет прямой команды сделать это.
«Судьбоносный шанс»
Берут 3 кости, сосредотачиваются на объекте своих грез и выкидывают их после активного встряхивания. Но сделать это надо таким образом, чтобы при выпадении из стаканчика они распределились в горизонтальный ряд. Тот кубик, который выпал по центру, отражает уже присутствующую или возможную взаимность. Хотя не факт, что вы выбрали или выберете самую достойную кандидатуру. Расположенный слева отражает отношение к вам некоего объекта. Так что при позитивном предсказании стоит внимательней присмотреться к своему окружению, может среди коллег и друзей и находится ваша половинка. Выпавшая с правой стороны кость указывает на ваши привязанности и если предсказание вам по душе, тогда стоит приложить любые усилия, чтобы добиться внимания объекта ваших воздыханий.
– Верность и стабильность в любви. Полное взаимопонимание. – Изменчивость и меркантильность партнера. Если брак и состоится, то будет или скоротечным или фиктивным. – Пылкая страсть, но ревность и выяснения обстоятельств станут ее постоянными спутниками. – Вероятен брачный союз. Если партер из творческой среды, то брак будет очень плодотворным и успешным. – Ваш избранник, скорее всего, невероятно скуп или расчетлив. При этом его педантичность может позволить ему достичь значительных высот в карьерном росте. – Чрезмерное самомнение мешает вам увидеть в толпе человека, который вам искренне симпатизирует.

Нечестное распределение
Считается, что если бросить идеальный кубик много-много раз, то количество выпавших ⚀, ⚁, ⚂, ⚃, ⚄, ⚅ разделится поровну. Сразу вопрос: много — это сколько? 10, 1000, 1000000? Математики не знают ответа. Возможно, вероятности сравняются, когда человечество уже закончит своё существование. Вам оно надо?
Второй момент: распределение вариантов во времени. Наверняка вы сталкивались с ситуацией, когда в одной из партий часто выпадает какая-то цифра, а на другой день — вообще не выпадает.
Вот пример несправедливости, которая часто возникает: Вася и Маша по очереди кидают кубик, и Васе постоянно выпадают ⚀, ⚁, ⚂, а Маше — ⚃, ⚄ и ⚅. В сумме получается, что каждая сторона кубика выпадает поровну. Но по факту — Маша будет всегда выигрывать, а Вася — проигрывать.
Вся штука в том, как распределяются выпадающие грани кубика во времени.
В идеале они должны распределяться поровну вне зависимости от:— количества игроков,— способа броска,— очерёдности ходов,— количества игр.
Понятно, что в реальности дело обстоит по-другому. Будете ли вы с этим мириться — зависит лично от вас, но я придерживаюсь мнения, что все игроки должны играть в равных условиях.
Устройство
Стандартные игральные кости — это маленькие кубики, чаще всего 1,6 см в поперечнике, грани которых пронумерованы от одного до шести, обычно круглыми точками, которые называются очками. Традиционно противоположные стороны кубика в сумме дают семь, причём грани 1, 2 и 3 имеют общую вершину, эти грани могут располагаться по часовой стрелке или против часовой стрелки по отношению к вершине. Если грани 1, 2 и 3 идут против часовой стрелки, кубик называется правым и наоборот. Западные кубики обычно правые, а китайские кубики — левые.
Очки на кубиках располагаются в особом порядке, как показано на рисунке справа. На азиатских кубиках порядок нанесения очков похож на европейский, но очки располагаются ближе к центру грани; одно очко крупнее других, а четыре очка окрашены в красный цвет. В некоторых из старинных наборов одно очко обозначалось углублением без окрашивания. Черная грань «один» и сочетание чёрного и белого цветов на грани «четыре» считались несчастливыми, поэтому красный, цвет удачи в китайской культуре, должен был нейтрализовать эту примету. Слово, обозначающее четыре (四 сы), в китайском языке созвучно слову «смерть» (死 сы), и считается несчастливым. Вероятно, что красные «четвёрки» имеют индийское происхождение.
Результат броска игральной кости считается случайным, так как в этом процессе присутствуют такие неопределённые факторы как движение руки бросающего и положение кости до броска. Таким образом, игральную кость можно считать прототипом генератора случайных чисел. Некоторые люди считают, что очки на гранях кубиков, выполненные в определенном стиле, вызывают небольшое смещение, но исследований для подтверждения данной идеи не проводилось. Кстати такое может быть справедливо для азиатских кубиков с увеличенным изображением одного очка. Кубики для казино выпускаются с залитой маркировкой, что служит подтверждением равномерного распределения случайных чисел.
Углы у некоторых кубиков закругляют не случайно: кубик получает слегка шарообразную форму, скольжение о поверхность стола увеличивается, он катится почти как шар и распределение вероятностей выпадения тех или иных чисел становится равномерным.
Игральные кости бросают по одному или группами, из руки или из предназначенного для этого устройства на ровную поверхность. На грани кубика, которая окажется верхней после его остановки, видно значение броска. Типичной игрой в кубики сегодня является крэпс, в которой бросают одновременно два кубика и делают ставки на сумму очков двух кубиков. Кубики часто используют для определения количества ходов на доске. Подобным методом определения пройденного расстояния фишки игрока по игровому полю пользуются в популярной настольной игре «Монополия».
Для настольных игр можно применять результаты броска игральной кости, сгенерированные на компьютере. Значения обычно определяются с помощью генератора псевдослучайных чисел, а затем отображаются на экране в виде какой-либо грани игральной кости. Возможен и вариант наоборот, когда броски игральных костей обеспечивают генерацию случайных чисел для компьютеров.
Теория вероятности игральной кости
Игральная кость бросается один раз
Когда бросают игральные кости, найти вероятность не сложно. Если предположить, что у нас правильная игральная кость, без различных ухищрений описанных выше, то вероятность выпадения каждой из его граней равна:
1 из 6 в дробном виде: 1/6в дестятичном виде: 0,1666666666666667
Игральная кость бросается 2 раза
Если бросают две игральные кости найти вероятность выпадения нужной комбинации можно перемножив вероятности выпадения нужной грани на каждой из костей:
1/6 × 1/6 = 1/36
Иными словами, вероятность будет равна 1 из 36. 36 – это количество вариантов, которые могут получится при выпадении нужного числа, сведем все эти варианты в таблицу и подсчитаем в ней сумму, образующую грани обеих кубиков.
| номер комбинации | комбинация | сумма |
| 1 | 2 | |
| 2 | 3 | |
| 3 | 4 | |
| 4 | 5 | |
| 5 | 6 | |
| 6 | 7 | |
| 7 | 3 | |
| 8 | 4 | |
| 9 | 5 | |
| 10 | 6 | |
| 11 | 7 | |
| 12 | 8 | |
| 13 | 4 | |
| 14 | 5 | |
| 15 | 6 | |
| 16 | 7 | |
| 17 | 8 | |
| 18 | 9 | |
| 19 | 5 | |
| 20 | 6 | |
| 21 | 7 | |
| 22 | 8 | |
| 23 | 9 | |
| 24 | 10 | |
| 25 | 6 | |
| 26 | 7 | |
| 27 | 8 | |
| 28 | 9 | |
| 29 | 10 | |
| 30 | 11 | |
| 31 | 7 | |
| 32 | 8 | |
| 33 | 9 | |
| 34 | 10 | |
| 35 | 11 | |
| 36 | 12 |
Вероятность выпадения нужной суммы при броске двух игральных костей:
| сумма | количество благоприятных комбинаций | вероятность, обыкновенные дроби | вероятность, десятичные дроби | вероятность, % |
| 2 | 1 | 1/36 | 0,0278 | 2,78 |
| 3 | 2 | 2/36 | 0,0556 | 5,56 |
| 4 | 3 | 3/36 | 0,0833 | 8,33 |
| 5 | 4 | 4/36 | 0,1111 | 11,11 |
| 6 | 5 | 5/36 | 0,1389 | 13,89 |
| 7 | 6 | 6/36 | 0,1667 | 16,67 |
| 8 | 5 | 5/36 | 0,1389 | 13,89 |
| 9 | 4 | 4/36 | 0,1111 | 11,11 |
| 10 | 3 | 3/36 | 0,0833 | 8,33 |
| 11 | 2 | 2/36 | 0,0556 | 5,56 |
| 12 | 1 | 1/36 | 0,0278 | 2,78 |
Этап наброски персонажа
Как известно, процессу объективации персонажа предшествует процедура создания его образа. В ходе последнего автор (художник) продумывает концепцию персонажа, его визуальную составляющую и характер героя.
В частности, необходимо:
Понять, для чего необходим персонаж и какие задачи он решает;
Оценить важность персонажа (основная или второстепенная роль, одиночка или часть группы);
Придумать историю данного персонажа (его биографию, возраст, национальность, профессию и др.);
Описать, как должен выглядеть персонаж (черты лица, форма тела, причёска, одежда и др.);
Продумать характер персонажа;
Выделить его яркую отличительную особенность;
Придумать, каким образом персонаж будет выражать эмоции и другое.
После того, как концепция персонажа сформирована, необходимо приступить к изучению сервисов, которые помогут сделать персонажа в любом стиле.
Цыганское гадание на костях
Цыганское гадание на костях обладает особой силой. У цыганок другое мнение на ритуал, поэтому они предпочитают гадать на костях по-своему. Для обряда необходим лист в форме круга, который делится на 12 секторов; на него бросают 3 кубика. Затем толкуют значение суммы, которое будет ответом:
- 3 – исполнение желания;
- 4 – разочарование;
- 5 – желание сбудется;
- 6 – духовное обогащение;
- 7 – глупые сплетни;
- 8 – несправедливость;
- 9 – прощение;
- 10 – семейная гармония;
- 11 – расставание;
- 12 – письмо;
- 13 – грусть;
- 14 – надежный друг;
- 15 – искушение;
- 16 – путешествие;
- 17 – гость;
- 18 – большая выгода и хорошая должность.
Гадание на кубиках
гадание с помощью игральных кубиков
Гадание на игральных костях (прогноз на день). Часть 1
Покер на костях

Техасский холдем и покер на костях имеют отличия
Во-первых, если в классическом покере игроки получают карманные карты и строят сильнейшие комбинации, то, чтобы играть в покер на костях, участники должны бросать кости и подсчитывать очки.
Во-вторых, в классическом покере игроки начинают ходить от баттона, а в покере на костях игру начинает участник, который смог выбросить больше всех очков.
В-третьих, существует ограничение по количеству игроков. Если в классическом покере за столом может находится до 10 человек, то к этой вариации количество участников может быть неограниченным.
Шаг третий. Собираем счётчик нажатий
Подключу кнопку одной ножкой к общему минусу, второй — к контакту 13 на Ардуино.

Я выбрал 13 контакт не случайно, на борту платы рядом с ним расположен оранжевый светодиод. Он будет гореть, когда кнопка отпущена и гаснуть, когда нажата. Почему, так происходит — расскажу в следующем проекте. Пока же воспользуюсь этим, чтобы проверить схему.


Изменю предыдущую программу так, чтобы значение счётчика менялось только при нажатии на кнопку.
Получился простой счётчик, похожими устройствами (их иногда называют кликеры) часто пользуются стюардессы, чтобы пересчитать пассажиров на борту самолёта.
Мошеничество с игральными костями
В раскопанных погребениях на всех континентах попадаются игральные кости, выполненные специально для нечестной игры. Они имеют форму неправильного куба. В результате наиболее часто выпадает самая длинная грань. Неправильность формы достигается стачиванием одной грани. Еще куб можно трансформировать в параллелепипед. Эти неправильные кости получили прозвище «болванок». Он считаются атрибутом шулерской игры, и, как правило, принадлежат мошенникам.
Современную болванку внешне невозможно отличить от обычной кости, поскольку она имеет форму идеального куба. Но в болванке одна или несколько граней имеют дополнительный вес. Такие грани и выпадают чаше других.
Еще одна уловка заключается в дубляже граней – одних достаточно много, другие напрочь отсутствуют. В результате одни цифры будут выпадать слишком часто, а другие – почти никогда. Эти кости называют «вершками и донышками». Такие изделиями пользуются мошенники с большим опытом и довольно ловкими руками. Обычный игрок зачастую не замечет, что его партнер ведет нечестную игру.
Некоторые мошенники много тренируются с нормальными костями. В результате у них получается выкидывать требуемые комбинации. С этой целью кости бросаются специальным способом, позволяющим одному или двум изделиям вращаться в вертикальной плоскости и ложиться на требуемую грань.
Другие жулики выбирают мягкую поверхность в виде одеяла или пальто. По такой поверхности кость катится наподобие катушки. В итоги боковые грани почти не выпадают, что приводит к нежелательным для соперника комбинациям.
Виды кубиков
Помимо того, что существуют разные виды игр с костями, есть и различные типы кубиков, с которыми каждому любителю «настольных костей» необходимо познакомиться.
Какие существуют кубики?
Чтобы хорошо бросить игральный кубик, нужно понимать, какого он вида, знать, какие тонкости есть у этого типа костяшек. Также существует специальный генератор кубиков, который поможет вам сделать хороший бросок. От того, как выглядит игральная кость, зависит ваша победа. Но, если вы хотите лучше в этом разбираться, можете купить себе набор кубиков разных видов и изучать их, пробовать играть.
- В первую очередь, это, конечно, стандартные игральные кубики, которые игроки видят в разных настольных играх.
- 2. Кубики с позами или экзотические кубики. Кости, которые принимать необычные позы.
- Зоккиэдр – крайне редко встречающаяся кость, которая имеет 100 граней. Его относят еще и к многогранным кубикам.
- Гоблинские кости (goblin dice), которые подходят в основном только в «Гоблинских костях».
- Кубики из слоновой кости.
- Серебряные кубики.
Несмотря на то, что все они кажутся очень разными, применяются они почти все одинаковы. Если вы хотите подробнее узнать о видах кубиков и о том, как проавильно бросить кубик, то можете посмотреть видео.
Вместо итогов
Полученные таблицы можно использовать для балансировки вероятностных значений в разрабатываемых играх. Ровно как можно с помощью данных расчетов более точно оценивать свои шансы на исход броска во время игры.
Продемонстрированный метод применим для получения таблиц к любому количеству бросков любых дайсов.
Кстати, с помощью разнообразных дайсов можно задавать довольно большой диапазон случайных значений. Например 2d6+1d4 даст нормальное распределение в диапазоне 3-16. А с помощью двух d10 можно задать линейное распределение 0-99, для этого один кубик должен отвечать за десятки, другой — за единицы. Такую комбинацию двух d10 называют «процентником».
Надеюсь, эти таблицы будут Вам полезны.
Юрий Исаев2015.07.27
Шаг второй. Выводим цифры
Пока индикатор зажигает отдельные сегменты, но чтобы вывести цифры нужно научиться зажигать комбинации. По принципу это напоминает заполнение почтового индекса. Попробуем вывести цифру 1. Для этого нужно определить, какие сегменты зажигать. Посмотрим схему подключения более внимательно.
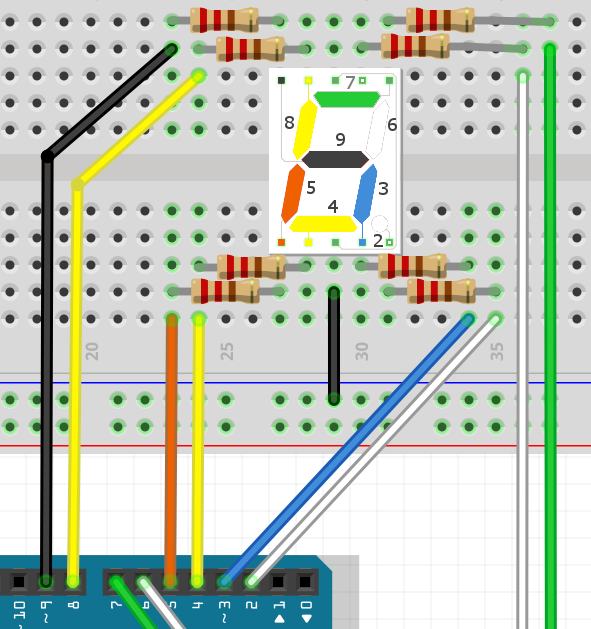
Чтобы вывести на экран цифру 1, нужно зажечь два правых сегмента. Они подключены белым и синим проводами к контактам 3 и 6. Изменю тестовую программу, чтобы она выводила на экран единицу.

Это уже что-то. Аналогично подберу сегменты, чтобы вывести остальные цифры. Соберу эту информацию в массив. Массив — это переменная, которая содержит сразу несколько значений. Каждое отдельное значение называется элементом массива. Такой элемент можно вывести, если знать его номер.
Мне нужен массив из 11 элементов: десять для цифр от 0 до 9 и один для точки.
Каждый элемент моего массива начинается со служебной комбинации символов 0b, которая означает, что элемент состоит из двоичных данных. А дальше идёт комбинация из восьми нулей или единиц. Они задают сегменты, которые будут гореть: 1 включит сегмент, 0 — выключит.
Запущу простую программу, которая будет последовательно выводить все элементы массива на экран.
Элементы готовы, остаётся добавить кнопку, которая будет управлять моим устройством.