Шаблоны геометрических фигур для вырезания из бумаги распечатать

Содержание

Как сделать правильный додекаэдр своими руками

Сегодня конструкция данной фигуры нашла свое отображение во многих вариантах художественного творчества, архитектуре и строительстве. Народные умельцы изготавливают из цветной или белой бумаги необыкновенные по красоте оригами в виде ажурных додекаэдров, а из картона делают оригинальные и прочее). В продаже можно приобрести уже готовые наборы, содержащие все необходимое для изготовления сувениров, но наиболее интересно произвести весь процесс работы своими руками, начиная от построения отдельных деталей и заканчивая сборкой готовой конструкции.

Материалы:

Для того, чтобы сделать правильный додекаэдр из картона, необходим собственно сам материал и подручные средства:

ножницы,
карандаш,
ластик,
линейка,
клей.

Хорошо иметь тупой нож или какое-либо приспособление для загибания припусков, но если их нет, то вполне подойдет металлическая линейка или те же ножницы.

Как сделать многогранник из бумаги: второй способ (adsbygoogle = window.adsbygoogle || []).push({});

Изготовьте два главных шаблона (фото 5):

— Первый. Нарисуйте на листе окружность и поделите ее поперек на две части. Одна будет основой для выкройки, дугу второй сразу сотрите для удобства. Поделите деталь на пять равных частей и ограничьте все радиусы поперечными отрезками. В результате получатся соединенные вместе пять одинаковых равнобедренных треугольников. Изобразите рядом примыкающую к среднему отрезку точно такую же полуокружность, только в зеркальном отражении. Полученная деталь при сворачивании выглядит как два конуса. Изготовьте таких аналогичных шаблонов всего шесть штук. Для их склеивания используется вторая деталь, которая будет помещаться вовнутрь.

— Второй. Этот шаблон – пятиконечная звезда. Выполните одинаковые двенадцать заготовок. Формируя многогранник, каждую из звезд с подогнутыми вверх концами помещают внутрь конусообразных деталей и приклеивают к граням.

Полный сбор фигуры получается путем соединения двойных блоков дополнительными отрезками бумаги, заводя их вовнутрь. Моделируя изделия, довольно проблематично сделать их разными по размеру. Готовые модели многогранников из бумаги не так-то просто увеличить. Для этого недостаточно просто сделать припуски по всем внешним границам. Нужно масштабировать отдельно каждую из граней. Только так возможно получить увеличенную копию первоначальной модели. Используя второй способ изготовления многогранника, сделать это намного проще, так как будет достаточно увеличить первоначальные заготовки, по которым уже выполняется нужное количество отдельных деталей.

Правильные многогранники

Все фигуры отличаются друг от друга различным количеством граней и их формой. Кроме этого, некоторые модели могут быть сложены из цельного листа (как описано в примере изготовления икосаэдра), другие – только путем сбора из нескольких модулей. Классическими считаются правильные многогранники. Из бумаги их делают, придерживаясь главного правила симметрии – наличия в шаблоне полностью одинаковых граней. Существует пять основных видов таких фигур. В таблице приведены сведения об их названиях, количестве и формах граней:

Название	Кол-во граней	Форма каждой грани
тетраэдр	4	треугольник
гексаэдр	6	квадрат
октаэдр	8	треугольник
додекаэдр	12	пятиугольник
икосаэдр	20	треугольник

Необходимый набор для сборки, схемы и развертки полигональной фигуры

Позаботьтесь о хорошем, удобном столе и стуле, нужно, что освещение падало из-за левого плеча, используйте настольную лампу. Чтобы не выпачкать стол клеем застелите его плёнкой или положите лист стекла с зашлифованными краями, чтобы не порезаться. Чтобы научиться складывать базовые изделия, вам понадобятся простые приспособления вроде ножниц, канцелярского ножа, клея ПВА и кисточки для его нанесения.

Отдайте предпочтение строительному клею ПВА — из всех разновидностей у него наиболее густая консистенция, он не портит бумагу, делая её мокрой и вязкой, как обычный. Используются разные виды — от папиросной до обычного картона. Новичкам советуют начинать с акварельной, в 200 грамм на м2 для крупных элементов и чертёжной разновидности 140-160 грамм – при разработке мелких частей.

Бумага для паперкрафта и клей для бумажных моделей

Основным материалом для создания является, естественно, обычная бумага, но так как она не сильно надёжная и хрупкая, советуем обратить внимание на полукартон, либо же обыкновенный картон. Детали из него более крепкие и придают готовому творению износостойкость

Удивительный кит с подсветкой—эксклюзивный ночник в спальне вашего ребёнка

У каждого мастера имеются свои секреты, вот и мы хотим поделиться с вами открытием.

Заготовки гораздо удобнее приклеивать узким двухсторонним скотчем. Он скрепляет моментально и угрозы “расклеиться” ваше творчество не потерпит.

Но также неплохой связующий предмет для элементов – клеевой раствор. Выбирайте вариант, который удобнее.

Модель из бумаги

Рабочий процесс создания проходит в несколько простых этапов. Перед началом процесса мастер определяется, какую фигурку он хочет сконструировать. На самом деле, можно смастерить практически любое изделие, но бумажное моделирование чаще предполагает такие варианты:

многогранники с выпуклыми и вогнутыми углами, геометрические фигуры
копии зданий в масштабе
макеты автомобилей премиум класса
танки, тяжелые орудия, бронемашины
поезда, корабли и подлодки, самолеты

Бумага для моделирования—основной рабочий материал

Следует уделить особое внимание её качеству! Для начального творчества лучше всего использовать обыкновенные листы формата А4, они имеют хорошее качество и является самой белоснежной по отношению к другим маркам. Плотность – 80 г/м

Советую приобретать специальную, для черчения.

Как построить развертку самостоятельно?

Пожалуй, помимо склеивания многогранника — хоть звездчатого, хоть платоновского, — еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр — это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр — простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней — равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр — это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.

Юный техник — для умелых рук 1986-12, страница 15

Секреты мастерства 3ВG3ДЧЯТЫв

МНОГОГРАННИКИ

Приглашаем вас на необычный урок геометрии, где вы научитесь построению звездчатых многогранников. В основе их лежат строгие математические закономерности.

Изготовив хотя бы одну такую звезду, вам, наверное, захочется «открыть» и другие. Своим разнообразием эти геометрические фигуры напоминают фантастические звезды, планеты, астероиды. Причем среди них, вероятно, есть и такие, которые еще никому не удавалось рассчитать и построить. Может, это Сделаете вы? Только начинать работу надо с азов.

Познакомившись с техникой изготовления простых звездчатых многогранников, вы сможете украсить рукотворными звездами актовый зал школы для новогоднего бала, свою комнату, елку. А почему бы не подарить такую звездочку ветерану, другу, не устроить выставку, где вы посоревнуетесь с друзьями в фантазии?

С глубокой древности математикам были известны пять выпуклых многогранников, которые называют Платоновыми телами. Это известные, наверное, каждому школьнику тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр. Этим фигурам в древности приписывали магические свойстза, они олицетворяли землю, воздух, воду, солнце, космос. Их только пять, больше при всем желании не придумаешь.

Каждая из этих фигур образована одинаковыми равносторонними многоугольниками: треугольниками, квадратами, пятиугольниками. Они и являются основой для построения любых звездчатых многогранников.

На рисунках 1—5 изображены пять простых многогранников: тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр. Здесь же даны чертежи их граней и возможные варианты разверток для их склейки. Такие грани довольно просто построить, зная основы геометрии.

Элементы для построения звездчатых фигур в основном такие же, только здесь каждая звезда может состоять и из разных граней (см. стр. 16).

Например, фигуры 6, 7, 8 составлены из одинаковых граней, а вот фигуры 9 и 10 — из двух видов граней. Из нескольких граней можно склеить заготовку для одной из вершин звезды, а после соединить их. Чаще всего грани образованы треугольниками либо квадратами. Сложнее форма граней, показанных на рисунках 8, 9, 10.

По приведенным здесь разверткам получится одна из вершин звезды. Остальные делаются так же.

У звезд 6, 7 и 8 все грани для одной заготовки одинаковы. У звезд 9 и 10 по две формы заготовок и, естественно, две формы вершин.

При изготовлении звезд по рисункам 9 и 10 вы убедитесь, что они получаются из взаимного пересечения двух видов более простых звезд. Так, звезда на рисунке 9 составлена из звезд 6 и 7; а звезда на рисунке 10 — из звезд 7 и 8-

Для изготовления звезд лучше всего применять тонкий цветной картон, наборы которого продаются в магазинах канцтоваров. Можно использовать плотную ватманскую бумагу, отходы от упаковок из картона. Для склеивания применяйте клей ПВА.

Из инструментов вам понадобятся: металлическая линейка, остро заточенный твердый карандаш, шило, чертилка или запиленный под шило гвоздь, вставленный в цанговый карандаш, кисть или тонкая вязальная спица для нанесения клея, ножницы прямые с острыми концами, большие и маленькие, и подкладка из картона, на которой вы будете работать.

Из плотной бумаги или картона сначала изготовьте шаблон одной грани, а лучше — заготовки целиком. С приведенных на наших рисунках разверток переколите их контуры. На изнаночной стороне картона соедините метки карандашом, а потом проведите по полученным линиям кончиком шила.

У каждой заготовки оставьте припуск (клапан) для склейки заготовок по ребрам. Согните заготовки по линиям сгиба на лицо, используя линейку.

Изготовиз полный комплект заготовок, приступайте к склейке вершин. Сначала нужно склеить каждую вершину отдельно. Клей наносится на края граней и на оставленный клапан, детали плотно прижимаются друг к другу до высыхания. После этого можно раскрасить одинаковые вершины. Причем у звезд 9 и 10 вершины разной формы должны быть разного цвета.

Для окончательной сборки звезды осталось склеить вершины друг с другом. При этом некоторые клапаны окажутся лишними, их обрезают. Клеить надо так, чтобы все клапаны оказались внутри. Если развертка выкроена правильно, каждая вершина точно встает на свое место. Трудно бывает приклеить последнюю вершину, но подумав, вы найдете выход из положения.

На этом можно было бы и закончите статью. Но все-таки хочется не ограничиваться рекомендациями, с которыми вы познакомились выше. Попробуйте придумать свою звезду! Какой она получится, посмотрим. Ждем от вас сообщений.

А. БИРЮКОВ, г. Курск Рисунки М. СИМАКОВА

■

Треугольник Пенроуза. Что это такое?

Нет ничего невозможного. Так можно сказать про треугольник Пенроуза. Это геометрически невозможная фигура, элементы которой не могут быть соединены. Все-таки невозможный треугольник стал возможным. Шведский живописец Оскар Реутерсвард в 1934 г. представил миру невозможный треугольник из кубиков. О. Реутерсвард считается первооткрывателем этой зрительной иллюзии. В честь этого события на почтовой марке Швеции напечатали позже этот рисунок.

А в 1958 г. математиком Роджером Пенроузом была напечатана публикация в английском журнале о невозможных фигурах. Именно он создал научную модель иллюзии. Роджер Пенроуз был невероятным ученым. Он проводил исследования в области теории относительности, а также увлекательной квантовой теории. Его наградили премией Вольфа совместно с С. Хокингом.

Известно, что художник Мауриц Эшер, находясь под впечатлением этой статьи, нарисовал свою изумительную работу — литографию «Водопад». Но возможно ли сделать треугольник Пенроуза? Как сделать, если это возможно?

Правильные и неправильные звездчатые многогранники

Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.

Поделка посложнее

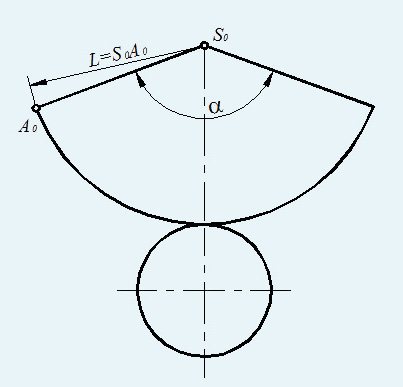
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.

Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!

Статья по теме: Подарочная корзина своими руками для мужчины: мастер-класс с фото

А вот ещё группа красавцев…

На рисунке изображен многогранник, называемый звездчатым октаэдром, получающийся продолжением граней октаэдра. Он был открыт Леонардо да Винчи, затем спустя почти сто лет переоткрыт И. Кеплером и назван им «Stella octangula» — звезда восьмиугольная.

Объединением каких двух многогранников он является? Что является их пересечением?

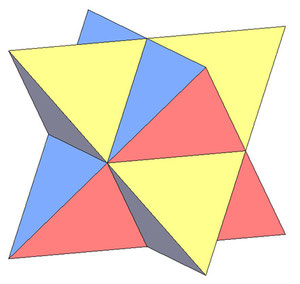
Ответ: Тетраэдров; октаэдр.

Какие боковые ребра должны быть у правильных пятиугольных пирамид, чтобы при добавлении их к граням додекаэдра с ребром a получился малый звездчатый додекаэдр?

Какие ребра должны быть у правильных треугольных пирамид, чтобы при удалении их из граней икосаэдра с ребром a получился большой додекаэдр?

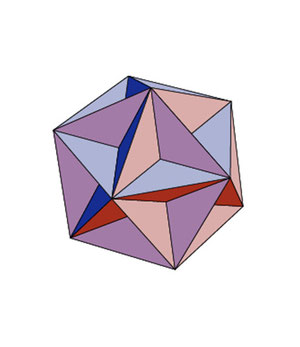
Какие ребра должны быть у правильных треугольных пирамид, чтобы при добавлении их к граням икосаэдра с ребром a получился большой звездчатый додекаэдр?

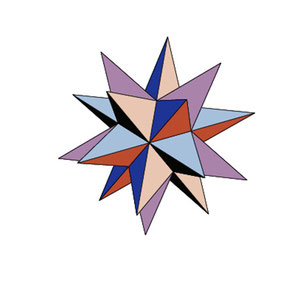
Вершинами какого многогранника являются вершины большого звездчатого додекаэдра?

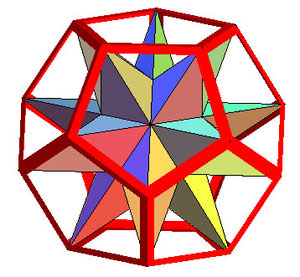
Как из большого додекаэдра можно получить многогранник, изображенный на рисунке?

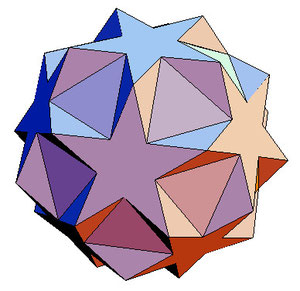
Ответ: Операцией усечения.

Трехмерные модели однородных многогранников и их звездчатых форм

Здесь можно увидеть трехмерные модели всех известных однородных многогранников: выпуклых Платоновых и Архимедовых тел, тел Кеплера — Пуансо и полуправильных звездчатых многогранников. В таблице представлен полный список многогранников и их некоторые характеристики. Для каждой трехмерной модели предусмотрено несколько вариантов раскраски, имеется также возможность просмотра строения граней и вершин. В специальном разделе галереи можно бегло ознакомиться с обзорными изображениями моделей.

Для каждого однородного многогранника можно породить как в трехмерном калейдоскопе огромное множество звездчатых форм, внешне чрезвычайно привлекательных. Достаточно рассмотреть изображения звезд в галерее, а также примеры звездоформ икосаэдра и кубоктаэдра. Для более сложных многогранников звездчатые формы практически не известны; этот сайт практически впервые дает возможность их увидеть и изучить. Для вас доступны два пути поиска новых многогранников: выбор какой-либо уже представленной на сайте звездчатой формы (а всего их тут более миллиона), либо целенаправленная сборка нового многогранника из отсеков в режиме ручного редактирования звездчатых форм.

Привлекательный внешний вид и огромное разнообразие форм однородных многогранников и их звездчатых форм делают перспективным применение оных как декоративных элементов. Вы можете сохранить на локальный диск любой многогранник для использования в собственных проектах, компьютерном дизайне и графике. Возможен экспорт трехмерных моделей в форматах 3DMAX (*.3ds), VRML (*.vrml), DirectX (*.x) и соответствующих анимированных изображений (*.gif, *.avi, *.swf). Вы можете создавать оригинальные электронные поздравительные открытки с изображениями многогранников. Достаточно выбрать самый красивый многогранник и подписать текст. Вашей открытке будет присвоен уникальный URL (интернет-ссылка), которую вы можете передать заинтересованным лицам. Новинка сезона — создание надписей прямо на гранях многогранника!

Многие великие и умные люди проявляли интерес к многогранникам. Во времена Пифагора учение о многогранниках было сакральным, тайной, доступной только избранным. В философской системе Платона важная роль отводилась правильным многогранникам. Архимед перечислил все полуправильные выпуклые многогранники. Кеплер придумал два звёздчатых правильных многогранника, затем Пуансо нашел ещё два, а Коши доказал: других правильных нет. Коксетер и другие только в середине 20 века перечислили остальные полуправильные невыпуклые многогранники. Ещё позднее удалось доказать, что список однородных многогранников полон. Что касается звездчатых форм сложных многогранников, то они практически никому не известны. Возможно именно Вам посчастливится найти интересно устроенный или особенно красивый многогранник! Тогда в галерее среди достойнейших мужей вы сможете занять свое почетное место.

Таблица — Список всех однородных многогранников

Бумажный цилиндр

Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.

Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.

Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!

Большой выбор развёрток простых геометрических фигур.

Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.

Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.

Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.

Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.

Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.

Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.

Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.

Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.

Что такое тетраэдр

С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги. Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью. В фигуре есть также четыре вершины и шесть ребер.

Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.

На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:

мостов;
перекрытий;
балок;
ферм;
пролетов зданий.

Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.

Пирамида из бумаги своими руками. схемы и способы изготовления