Содержание
Конструкция зубчатого колеса
Встречается просто огромное количество разновидностей шестерен, все они характеризуются своими определенными особенностями. Среди конструкционных особенностей отметим следующие моменты:
- При изготовлении цилиндрических и конических шестерен с прямым зубом рабочая часть создается заодно целое с валом. Это связано с тем, что размеры конструкции существенно уменьшаются. За счет создания такой конструкции можно получить деталь с высокой точностью и износостойкостью.
- Встречаются и шестерни насадного типа. Они весьма распространены в случае, когда диаметр рабочей части большой. За счет установки насадного варианта исполнения есть возможность проводить обслуживание конструкции.
- При диаметре менее 500 мм изделие получается методом ковки и отливки, а также при применении технологии сварки. Вариант исполнения более 500 мм изготавливаются методов отливки и сварки.
- Клепанные или свертные колеса могут устанавливаться в случае, если есть необходимости в экономии используемого материала.
Конструктивными особенностями подобного варианта исполнения можно назвать:
- В качестве заготовки применяется диск определенной толщины.
- В центральной части есть посадочное отверстие с прорезью для шпонки. Как правило, оно имеет достаточно большую кайму.
- Рабочая часть представлена зубьями, которые могут быть расположены прямо или под углом. При этом геометрия зуба может существенно отличаться, все зависит от области эксплуатации.
Изготовление цилиндрических зубчатых колес проводится при применении специального оборудования. Примером можно назвать зубонарезные станки, которые работают по методу обкатки. Стоит учитывать, что процесс изготовления конических зубчатых колес существенно отличается.
Типы зубчатых передач
Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.
Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.
Расчет в Excel координат точек профиля зуба.
Для выполнения громоздких и достаточно сложных расчетов запускаем программу MS Excel. Выполнить этот расчет можно и в программе Calc из бесплатных офисных пакетов Apache OpenOffice или LibreOffice.
Представленный далее алгоритм расчета адаптирован для колес с наружными зубьями. Для колес с внутренними зубьями его можно применить после незначительных поправок.
Для косозубых колес профиль строится для торцевого сечения.
Исходные данные:
Профиль зуба будем «нарезать» реечным инструментом – гребенкой или червячной фрезой. Параметры и коэффициенты исходного контура возьмем по ГОСТ13755-81. Посмотреть на чертеж исходной рейки и понять, что это такое можно здесь.
Первые четыре параметра в ячейках D3-D6 характеризуют исходный контур.
Следующие пять исходных данных в ячейках D7-D11 являются «паспортом» зубчатого колеса, представляя о нем исчерпывающую информацию.
Алгоритм расчетов:
Результаты расчетов угла профиля и всех диаметров получены по следующим формулам:
10. αt =arctg (tg ( α )/cos ( β ))
11. dа = d +2* m *( ha * + x — Δy )
12. d = m * z /cos ( β )
13. db = d *cos ( αt )
14. df = dа -2* m *(2* ha* + c* — Δ y )
Часть профиля зуба – это эвольвента основной окружности диаметром db. Таким образом, эвольвента может существовать в зубчатом колесе от диаметра основной окружности до диаметра вершин зубьев!
Вторая часть профиля зуба – переходная кривая от эвольвенты до диаметра впадин.
Я выбрал количество точек n каждой из кривых для своего примера равное 100, посчитав его достаточным для требующейся точности построения. Если вы захотите его изменить, то вам нужно будет соответственно расширить или сузить таблицу «Координаты точек профиля зуба», которая сдержит 100 строк ( imax=n ).
Результаты вспомогательных констант определены по формулам:
16. D =2* m *(( z /(2*cos ( β )) — (1- x )) 2 +((1- x )/tg ( αt )) 2 ) 0,5
17. hdy =( da – db )/( n -1)
18. h γ = γ1/( n -1)
19. h da =2* X э1 /( n -1)
20. C =(π/2+2* x *tg ( α ))/ z +tg ( αt ) — αt
21. y=1- ( ρf * )*sin ( αt ) – x
22. x=π/(4*cos ( β ))+( ρf * )*cos ( αt )+tg ( αt )
Подготовка завершена, можно выполнить расчет в Excel промежуточных данных и непосредственно координат точек профиля зуба.
Значения в таблице рассчитаны по формулам:
γ1 =π/2- αt
γ (i+1) = γ i – h γ
Ai = z /(2*cos( β )) – y — ( ρf * )*cos ( γ i )
Bi = y *tg( γ i ))+( ρf * )*sin ( γ i)
φi =(2*cos( β )/ z )*( x + y *tg ( γ i ))
Yэi =( dyi /2)*cos ( Di )
Xэi = Y эi *tg ( Di )
Yпкi =( Ai *cos ( φi )+ Bi *sin ( φi ))* m
Xпкi =( Ai *sin ( φi ) -Bi*cos ( φi ))* m
Xda1 =- X э1
Xda (i+1) = Xdai + h da
Ydai =(( dа /2) 2 — Xdai 2 ) 0,5
После того, как расчет в Excel выполнен, запускаем мастера диаграмм и строим точечные графики по полученным координатам. О том, как это делается подробно описано тут.
На скриншоте выше синим цветом показан наружный диаметр, темно-синим изображены эвольвенты, лиловым – переходные кривые.
Оси X и Y пересекаются в центре колеса — это точка начала координат.
Excel построил профиль зуба! Задача решена.
Изменяя исходные данные можно мгновенно оценить визуально изменения профиля зуба и увидеть подрезку ножки или заострение вершины при применении смещения контура.
Модуль зубчатого колеса
Универсальным понятием, позволяющим определить геометрические параметры деталей, выступает модуль зубчатой передачи. Его значение равно длине дуги в миллиметрах, приходящейся на один зуб колеса. Конкретное значение определяется по делительной окружности. Ее численно подбирают таким образом, что бы значение модуля совпадало с одним из общепринятых значений, найти которые можно в специальной литературе. В отечественной практике стандартные модули зубчатых колес нормированы в ГОСТ 9563-60. При проектировании шестерен обычно задаются значением этого параметра, а от него легко рассчитают все множество других. Исходными данными для определения требуемого модуля зубчатого колеса выступают расчеты прочности, призванные обеспечить требуемую мощность механической передачи.
Модуль зубчатого колеса связан с целым набором производных параметров. Используя несложные формулы расчета и значение необходимого числа зубьев, можно получить окружной шаг, диаметры верши и впадин, толщину зуба и ширину впадины по делительной окружности.
В зарубежной литературе аналогом отечественного модуля выступает питч. По своей сути это обратная к модулю зацепления величина, приведенная к дюймовой системе измерений. Аналогично для питчей разработаны специальные таблицы, содержащие нормированные значения параметра.
Что представляет собой шестерня
Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.

Шестеренчатые передачи также имеют свою классификацию:
- Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
- Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
- Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
- Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.
Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.
При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.
Почему шестеренку называют так?
Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».
Конструкция зубчатого колеса
Встречается просто огромное количество разновидностей шестерен, все они характеризуются своими определенными особенностями. Среди конструкционных особенностей отметим следующие моменты:
- При изготовлении цилиндрических и конических шестерен с прямым зубом рабочая часть создается заодно целое с валом. Это связано с тем, что размеры конструкции существенно уменьшаются. За счет создания такой конструкции можно получить деталь с высокой точностью и износостойкостью.
- Встречаются и шестерни насадного типа. Они весьма распространены в случае, когда диаметр рабочей части большой. За счет установки насадного варианта исполнения есть возможность проводить обслуживание конструкции.
- При диаметре менее 500 мм изделие получается методом ковки и отливки, а также при применении технологии сварки. Вариант исполнения более 500 мм изготавливаются методов отливки и сварки.
- Клепанные или свертные колеса могут устанавливаться в случае, если есть необходимости в экономии используемого материала.
Конструктивными особенностями подобного варианта исполнения можно назвать:
- В качестве заготовки применяется диск определенной толщины.
- В центральной части есть посадочное отверстие с прорезью для шпонки. Как правило, оно имеет достаточно большую кайму.
- Рабочая часть представлена зубьями, которые могут быть расположены прямо или под углом. При этом геометрия зуба может существенно отличаться, все зависит от области эксплуатации.
Изготовление цилиндрических зубчатых колес проводится при применении специального оборудования. Примером можно назвать зубонарезные станки, которые работают по методу обкатки. Стоит учитывать, что процесс изготовления конических зубчатых колес существенно отличается.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Документы
Сортировать по :
названию | дате | популярности
Шестерня m=2, Z=33
| Дата добавления: | 20.08.2010 |
| Дата изменения: | 20.08.2010 |
| Размер файла: | 42.51 Кбайт |
| Скачиваний: | 886 |
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2, Z=24
| Дата добавления: | 08.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 41.73 Кбайт |
| Скачиваний: | 935 |
Шестерня цилиндрическая, используется в станке 2А554.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2, Z=20
| Дата добавления: | 15.06.2010 |
| Дата изменения: | 13.08.2010 |
| Размер файла: | 44.27 Кбайт |
| Скачиваний: | 863 |
Шестерня используется в токарно-винторезном станке 163.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2, Z=18
| Дата добавления: | 02.11.2010 |
| Дата изменения: | 02.11.2010 |
| Размер файла: | 35.75 Кбайт |
| Скачиваний: | 826 |
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=10, Z=15
| Дата добавления: | 20.08.2010 |
| Дата изменения: | 20.08.2010 |
| Размер файла: | 40.63 Кбайт |
| Скачиваний: | 881 |
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=1, Z=9
| Дата добавления: | 31.08.2010 |
| Дата изменения: | 31.08.2010 |
| Размер файла: | 35.98 Кбайт |
| Скачиваний: | 845 |
Шестерня используется в станке 1Е61
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=1, Z=35
| Дата добавления: | 04.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 42.91 Кбайт |
| Скачиваний: | 897 |
Чертеж шестерни цилиндрической на двигатель смазки станка 1М553.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=1, Z=35
| Дата добавления: | 01.11.2010 |
| Дата изменения: | 01.11.2010 |
| Размер файла: | 37.17 Кбайт |
| Скачиваний: | 835 |
Шестерня применяется в станке 3М184
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=1, Z=28
| Дата добавления: | 01.11.2010 |
| Дата изменения: | 01.11.2010 |
| Размер файла: | 42.45 Кбайт |
| Скачиваний: | 873 |
Шестерня применяется в станке 3М184
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=1, Z=102
| Дата добавления: | 01.11.2010 |
| Дата изменения: | 01.11.2010 |
| Размер файла: | 35.47 Кбайт |
| Скачиваний: | 889 |
Шестерня применяется в станке 3М184
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Классификация
По направлению витка передачи в большинстве своем бывают правыми. Иногда встречается левое направление нити.
Червячные зацепления классифицируются по форме наружной поверхности червяка:
- цилиндрические;
- глобоидные.
Вогнутая поверхность ведущей детали увеличивает количество зубьев, находящихся одновременно в зацеплении. В результате возрастает КПД и мощность передачи. Недостаток глобоидных червяков в сложности изготовления. Витки должны быть одинаковой высоты при вогнутой наружной поверхности.
По форме нити резьбы различают червяки:
- архимедов;
- конволютный;
- нелинейный.
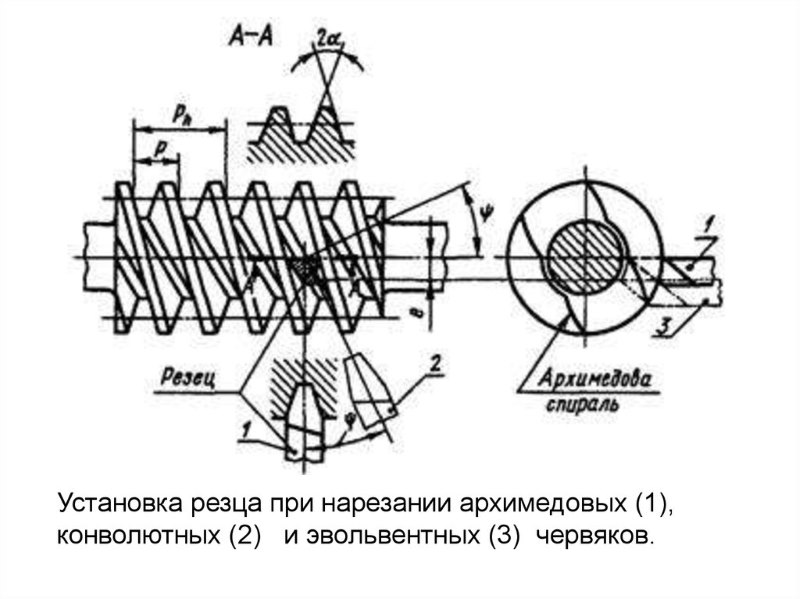
Архимедов червяк отличается прямой в сечении эвольвентой. У конволютного конфигурация выпуклая, близкая к форме обычной шестерни. Нелинейные профили имеют выпуклую и вогнутую поверхность.
Зубчатое колесо имеет зуб наклонный обратной конфигурации, по форме совпадающий с впадиной между нитями.
Расположение червяка относительно колеса может быть:
- верхнее;
- боковое;
- нижнее.
Верхнее оптимально подходит для скоростных передач. Боковое наиболее компактное. При картерном способе смазки – масло находится в поддоне и нижняя деталь, вращаясь, смазывает остальные, удобнее нижнее расположение червяка.
Червячные колеса относятся к косозубым. Оси деталей располагаются обычно под углом 90°. В сильно нагруженных механизмах угол может быть 45°.
Зубчатые колеса по профилю зуба делят:
- роликовые;
- вогнутые;
- прямые.
По типу они могут быть:
- с непрерывным вращением – полные;
- зубчатый сектор.
Сектор может быть разной величины, от половины круга, до рабочей длины короче червяка.
Передаточное число зубчатой передачи
Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.
Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.
Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.
Пример:
Момент входной = 1,5 Н∙м, Скорость входная = 100 об/с,
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с.
Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.
Документы
Сортировать по :
названию | дате | популярности
Шестерня m=2.5, Z=35
популярный!
| Дата добавления: | 08.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 55.37 Кбайт |
| Скачиваний: | 1299 |
Чертеж шестерни используемой в станке 2А554.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Блок-шестерня m=2.5, Z1=33, Z2=19
популярный!
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 51.48 Кбайт |
| Скачиваний: | 1131 |
Чертеж блок-шестерни. Применяется в станке 2Л53У.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=20
популярный!
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 41.4 Кбайт |
| Скачиваний: | 1089 |
Чертеж шестерни с посадкой на шпонку. Используется в станке 2Л53У.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=51
популярный!
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 50.61 Кбайт |
| Скачиваний: | 1063 |
Чертеж шестерни с посадкой на шлицы. Применяется в станке 2Л53У.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Вал-шестерня m=3, Z=21
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 49.69 Кбайт |
| Скачиваний: | 941 |
Чертеж вал-шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=30
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 43.64 Кбайт |
| Скачиваний: | 939 |
Чертеж шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=44
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 43.79 Кбайт |
| Скачиваний: | 946 |
Чертеж шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=3, Z=24
популярный!
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 43.27 Кбайт |
| Скачиваний: | 1016 |
Чертеж шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=56
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 43.82 Кбайт |
| Скачиваний: | 995 |
Чертеж шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=39
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 41.27 Кбайт |
| Скачиваний: | 920 |
Чертеж шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Изготовление зубчатых колёс
Существует несколько методов изготовления колес.
Метод обката
В настоящее время является наиболее технологичным, а поэтому и самым распространённым способом изготовления зубчатых колёс. При изготовлении зубчатых колёс могут применяться такие инструменты, как гребёнка, червячная фреза и долбяк.
Метод обката с применением гребёнки
Изготовление шестерни.
Изготовление зубчатого колеса.

Режущий инструмент, имеющий форму зубчатой рейки, называется гребёнкой. На одной стороне гребёнки по контуру её зубьев затачивается режущая кромка.
Заготовка накатываемого колеса совершает вращательное движение вокруг оси. Гребёнка совершает сложные перемещения, состоящие из поступательного движения перпендикулярно оси колеса и возвратно-поступательного движения (на анимации не показано), параллельного оси колеса для снятия стружки по всей ширине его обода. Относительное движение гребёнки и заготовки может быть и иным, например, заготовка может совершать прерывистое сложное движение обката, согласованное с движением резания гребёнки.
Заготовка и инструмент движутся на станке друг относительно друга так, как будто происходит зацепление профиля нарезаемых зубьев с исходным производящим контуром гребёнки.
Метод обката с применением червячной фрезы
Помимо гребёнки в качестве режущего инструмента применяют червячную фрезу. В этом случае между заготовкой и фрезой происходит червячное зацепление.

Метод обката с применением долбяка
Зубчатые колёса также долбят на зубодолбёжных станках с применением специальных долбяков.
Зубодолбёжный долбяк представляет собой зубчатое колесо, снабжённое режущими кромками. Поскольку срезать сразу весь слой металла обычно невозможно, обработка производится в несколько этапов.
При обработке инструмент совершает возвратно-поступательное движение относительно заготовки. После каждого двойного хода, заготовка и инструмент поворачиваются относительно своих осей на один шаг. Таким образом, инструмент и заготовка как бы «обкатываются» друг по другу. После того, как заготовка сделает полный оборот, долбяк совершает движение подачи к заготовке. Этот процесс происходит до тех пор, пока не будет удалён весь необходимый слой металла.

Литейная форма для бронзового храпового колеса (Китай, династия Хань. (206 до н. э. — 220 н. э.)).
Метод копирования (Метод деления)
Дисковой или пальцевой фрезой нарезается одна впадина зубчатого колеса. Режущая кромка инструмента имеет форму этой впадины. После нарезания одной впадины заготовка поворачивается на один угловой шаг при помощи делительного устройства, операция резания повторяется.
Метод применялся в начале XX века. Недостаток метода состоит в низкой точности: впадины изготовленного таким методом колеса сильно отличаются друг от друга.
Горячее и холодное накатывание
Процесс основан на последовательной деформации нагретого до пластического состояния слоя определенной глубины заготовки зубонакатным инструментом. При этом сочетаются индукционный нагрев поверхностного слоя заготовки на определенную глубину, пластическая деформация нагретого слоя заготовки для образования зубьев и обкатка образованных зубьев для получения заданной формы и точности.
Изготовление конических колёс

Технология изготовления конических колёс теснейшим образом связана с геометрией боковых поверхностей и профилей зубьев.
Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, так как размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, можно использовать только для черновой прорезки впадин или для образования впадин колёс не выше восьмой степени точности.
Для нарезания более точных конических колёс используют способ обкатки в станочном зацеплении нарезаемой заготовки с воображаемым производящим колесом. Боковые поверхности производящего колеса образуются за счёт движения режущих кромок инструмента в процессе главного движения резания, обеспечивающего срезание припуска. Преимущественное распространение получили инструменты с прямолинейным лезвием. При прямолинейном главном движении прямолинейное лезвие образует плоскую производящую поверхность. Такая поверхность не может образовать эвольвентную коническую поверхность со сферическими эвольвентными профилями. Получаемые сопряжённые конические поверхности, отличающиеся от эвольвентных поверхностей, называют квазиэвольвентными.
Документы
Сортировать по :
названию | дате | популярности
Шестерня m=2.5, Z=35
| Дата добавления: | 20.08.2010 |
| Дата изменения: | 20.08.2010 |
| Размер файла: | 47.06 Кбайт |
| Скачиваний: | 933 |
Шестерня m=2.5, Z=35 применяется в станке 2С550
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=30
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 43.64 Кбайт |
| Скачиваний: | 939 |
Чертеж шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=29
| Дата добавления: | 01.11.2010 |
| Дата изменения: | 01.11.2010 |
| Размер файла: | 37.3 Кбайт |
| Скачиваний: | 898 |
Шестерня применяется в станке 5А05
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=25
| Дата добавления: | 20.08.2010 |
| Дата изменения: | 20.08.2010 |
| Размер файла: | 42.9 Кбайт |
| Скачиваний: | 912 |
Шестерня m=2.5, Z=25 используется в станке 2С550
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=25
| Дата добавления: | 20.08.2010 |
| Дата изменения: | 20.08.2010 |
| Размер файла: | 66.01 Кбайт |
| Скачиваний: | 893 |
Шестерня m=2.5, Z=25 используется в станке 2С550
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=20
популярный!
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 41.4 Кбайт |
| Скачиваний: | 1089 |
Чертеж шестерни с посадкой на шпонку. Используется в станке 2Л53У.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2.5, Z=17
| Дата добавления: | 07.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 42.32 Кбайт |
| Скачиваний: | 912 |
Чертеж шестерни, применяется в станке 2А43.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2, Z=54
| Дата добавления: | 15.06.2010 |
| Дата изменения: | 13.08.2010 |
| Размер файла: | 41.93 Кбайт |
| Скачиваний: | 896 |
Шестерня используется в станке 163.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2, Z=50
популярный!
| Дата добавления: | 01.12.2010 |
| Дата изменения: | 01.12.2010 |
| Размер файла: | 35.19 Кбайт |
| Скачиваний: | 1042 |
Шестерня используется в притирочном станке.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Шестерня m=2, Z=36
| Дата добавления: | 09.08.2010 |
| Дата изменения: | 13.08.2010 |
| Размер файла: | 48 Кбайт |
| Скачиваний: | 958 |
Шестерня m=2, Z=36, используется в станке СС2В05.
Чертежи выполнены в двух форматахcdw — Компас 9 СП2dwg — Autocad 2000
-
Скачать
-
Подробнее
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
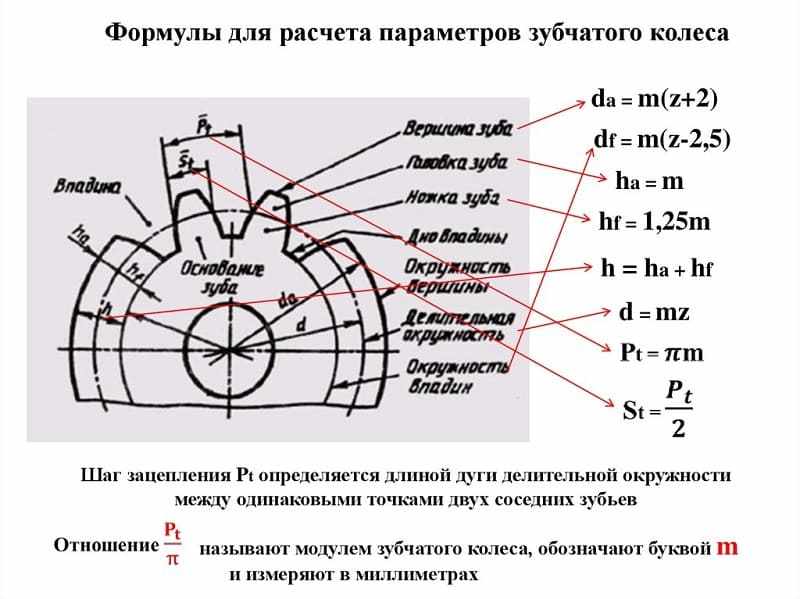
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
π×D=t× z,
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D e получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
De=m×z+2m = m(z+2),
откуда вытекает:
Диаметр окружности впадин D i соответствует D e за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Выполнив подстановку в правой части равенства, имеем:
D i = m×z-2×1,25m = m×z-2,5m;
что соответствует формуле:
D i = m(z-2,5m).
Полная высота:
и если выполнить подстановку, то получим:
h = 1m+1,25m=2,25m.
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s в, получаем формулы для ширины впадины
- для отлитых зубцов: s в =πm-1,53m=1,61m:
- для выполненных путем фрезерования- s в = πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
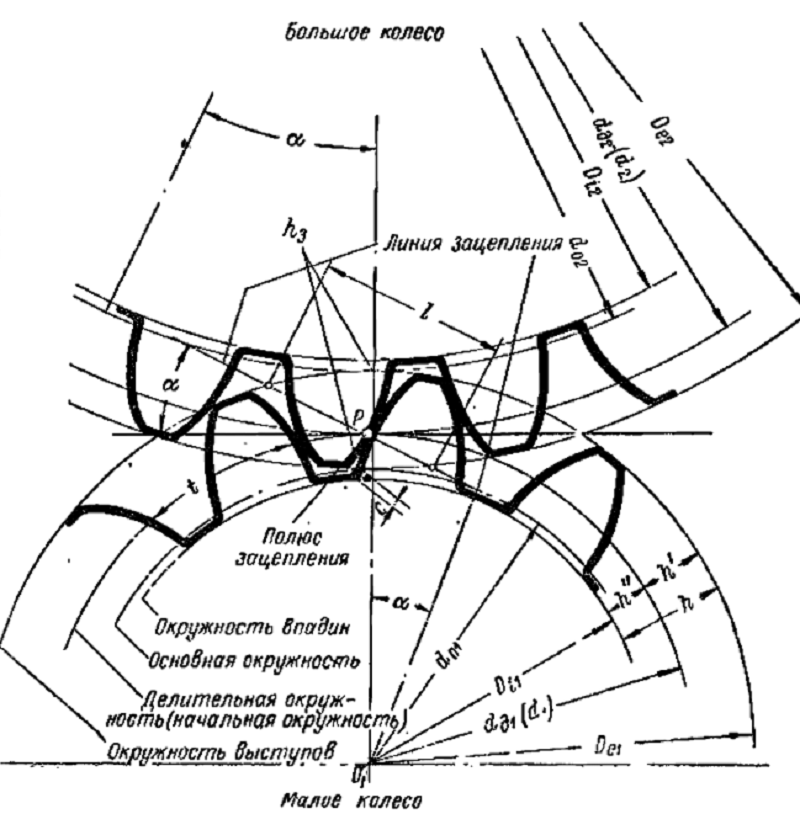
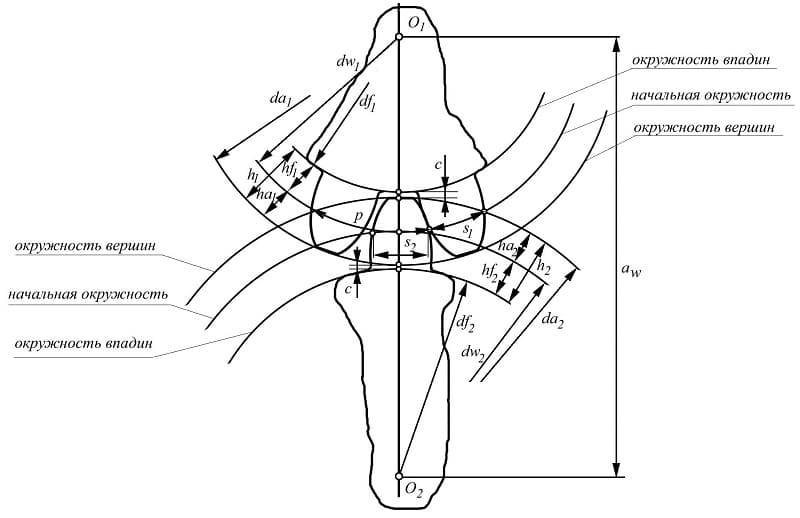
Диаметры окружностей
Рассмотрение геометрии зубчатых пар невозможно без определения диаметров. На каждой детали их выделяется несколько. Широкое распространение имеет диаметр окружности по выступам, иногда называемый диаметром вершин. Он определяет максимальные габариты диска колеса. Его противоположностью считается диаметр окружности впадин. Разность этих величин, поделенная пополам, дает полную длину зуба. Но этот параметр в чистом виде не используется. При расчетах принято выделять высоту головки и ножки зуба. Граница, отделяющая два этих понятия, называется делительной окружностью зубчатого колеса. Диаметр данной окружности выполняет функцию опорного параметра при выполнении расчетов геометрии, так как именно по ней определяется окружной шаг и модуль зацепления. Еще один диаметральный параметр, называемый основной окружностью, описывает теоретическую кривую, которая является базой при построении эвольвенты. Диаметр основной окружности используется для построения конкретного профиля зуба.