Отклоняемый вектор тяги

Содержание

Примеры работы

Самолет

Морской лунь FA.2 ZA195 переднее (холодное) сопло векторной тяги

Примером двумерного вектора тяги является Роллс-Ройс Пегас двигатель, используемый в Хоукер Сиддли Харриер, а также в AV-8B Harrier II вариант.

Широкого распространения вектора тяги для повышения маневренности в западных серийных истребителях не произошло до развертывания Локхид Мартин F-22 Raptor Реактивный истребитель пятого поколения 2005 года с форсажем, двумерным вектором тяги Пратт и Уитни F119 турбовентилятор.

В Lockheed Martin F-35 Lightning II при использовании обычного ТРДД с дожиганием (Pratt & Whitney F135) для облегчения работы на сверхзвуковых частотах, вариант F-35B, разработанный для совместного использования Корпус морской пехоты США, королевские воздушные силы, Королевский флот, и Итальянский флоттакже включает в себя вертикально установленный выносной вентилятор низкого давления с приводом от вала, который приводится в действие через муфту во время посадки от двигателя. Как выхлоп от этого вентилятора, так и вентилятор главного двигателя отклоняются соплами с вектором тяги, чтобы обеспечить соответствующее сочетание подъемной силы и тяги. Он не предназначен для повышения маневренности в бою, только для СВВП эксплуатации, а F-35A и F-35C вообще не используют вектор тяги.

В Сухой Су-30МКИ, производится Индией по лицензии на Hindustan Aeronautics Limited, находится на активной службе в ВВС Индии. TVC делает самолет высокоманевренным, способным без сваливания достигать почти нулевой воздушной скорости на больших углах атаки и выполнять динамичный пилотаж на малых скоростях. В Су-30МКИ питается от двух АЛ-31ФП дожигание турбовентиляторы. Сопла TVC МКИ установлены на 32 градуса наружу к продольной оси двигателя (т. Е. В горизонтальной плоскости) и могут отклоняться на ± 15 градусов в вертикальной плоскости. Это дает штопор эффект, значительно увеличивая возможность поворота самолета.

Несколько компьютерных исследований добавляют вектор тяги к существующим пассажирским авиалайнерам, таким как Boeing 727 и 747, для предотвращения катастрофических отказов, в то время как экспериментальные X-48C может быть реактивным в будущем.

Другой

Примеры ракет и ракет, использующих вектор тяги, включают в себя обе большие системы, такие как Ракетный ускоритель космического челнока (SRB), С-300П (СА-10) ракета земля-воздух, UGM-27 Polaris ядерный баллистическая ракета и РТ-23 (СС-24) баллистические ракеты и меньшее боевое оружие, такое как Swingfire.

Принципы управления вектором воздушной тяги были недавно адаптированы к военным морским применениям в виде быстрого водометного рулевого управления, обеспечивающего сверхманевренность. Примеры: быстроходный патрульный катер Dvora Mk-III, Ракетный катер класса Хамина и ВМС США Прибрежные боевые корабли.

Авиация Управление вектором тяги — Газодинамическое управление вектором тяги

Высокой эффективности управления вектором тяги можно добиться с помощью газодинамического управления вектором тяги за счет асимметричной подачи управляющего воздуха в тракт сопла.

Газодинамическое сопло использует «струйную» технику для изменения эффективной площади сопла и отклонения вектора тяги, при этом механически сопло не регулируется. В этом сопле отсутствуют горячие высоконагруженные подвижные детали, оно хорошо компонуется с конструкцией ЛА, что уменьшает массу последнего.

Внешние контуры неподвижного сопла могут плавно вписываться в обводы самолета, улучшая характеристики малой заметности. В этом сопле воздух от компрессора может направляться в инжекторы в критическом сечении и в расширяющейся части для изменения соответственно критического сечения и управления вектором тяги.

В МАИ были проведены экспериментальные работы по управлению вектором тяги за счет взаимодействия «дешевого» атмосферного воздуха с основной струей. За счет перераспределения эжектируемого через боковые каналы воздуха происходит отклонение основной струи двигателя. Были разработаны и испытаны малогабаритные модельные образцы устройств с применением твердотопливных газогенераторов в качестве источников сжатого газа. В боковых каналах плоского эжектора, связанных с атмосферой, были установлены клапаны с электромагнитным управлением. Температура газа в газогенераторе составляла 2600 К, рабочее давление до 5..7 МПа. Развиваемая управляемая тяга 1.0 кН. Время переключения тяги из одного крайнего положения в другое не превышало 0.02 с. Удельная мощность управляющего сигнала на единицу тяги составляла не более 0.05..0.7 Вт/кгс.

Проведенные испытания показали возможность отклонения вектора тяги на углы ±20° при прилипании струи к боковой стенке эжекторного сопла.

В ЦИАМ проводились предварительные исследования на физико-математической модели сопла с газодинамическим управлением вектором тяги двигателя для учебно-тренировочного самолета в 2D постановке. В ТРДД для УТС наличие второго контура со сжатым и относительно холодным воздухом, отсутствие необходимости регулирования проходных сечений облегчает реализацию концепции сопла с газодинамическим управлением вектором тяги.

В исследуемом сопле выходной канал второго контура разделен продольными перегородками на четыре сектора с установленными на входе в каждый сектор устройствами регулирования расхода воздуха. Это сопло на режиме осевого истечения представляет собой сопло эжекторного типа с «жидкой» стенкой, однако в нем эжектируемый воздух поступает не из атмосферы, а из-за вентилятора, следовательно, имеет достаточно высокое давление. Стенка сопла первого контура разорвана сразу за его критическим сечением, поэтому выходящая из него струя газа расширяется, постоянно уменьшая к выходу площадь струи второго контура.

Для принятых значений параметров на этом режиме качество рассматриваемого варианта может быть выше, чем при раздельном истечении. Это возможно благодаря замене двух поверхностей трения на «жидкую» стенку, а также благодаря выравниванию поля скоростей на выходе вследствие частичного смешения потоков. Кроме того, такая схема сопла может обеспечить улучшенное протекание рабочей линии вентилятора на дроссельных режимах.

Для получения максимального отклонения потока один сектор подвода воздуха второго контура полностью перекрывается. В результате расход через второй сектор возрастает в два раза.

Отклонение струи происходит благодаря:

неосевому истечению струи воздуха второго контура и действию ее на поток первого контура под углом в направлении к оси сопла;
формированию на срезе сопла первого контура вблизи перекрытого сектора течения Прандтля-Майера и работе сопла как сопла с косым срезом.

В настоящее время ведутся работы над 3D вариантом такого сопла и сопла с использованием атмосферного воздуха. По предварительным оценкам рассматриваемые схемы сопел способны обеспечить эффективный угол отклонения вектора тяги ±20°.

Конструкция струйного сопла УВТ для двигателя[править | править код]

Конструкции струйных сопел отличаются разнообразием силовых и газодинамических схем.

Рассмотрим конструкцию с использованием расширяющейся сверхзвуковой частью сопла для создания боковой силы тяги. С этой целью выходной раструб сопла переводится в режим перерасширения и с одной из сторон сопла, на его боковой поверхности открываются отверстия для доступа атмосферного воздуха. При этом струя из двигателя прилипает к противоположной стороне сопла.

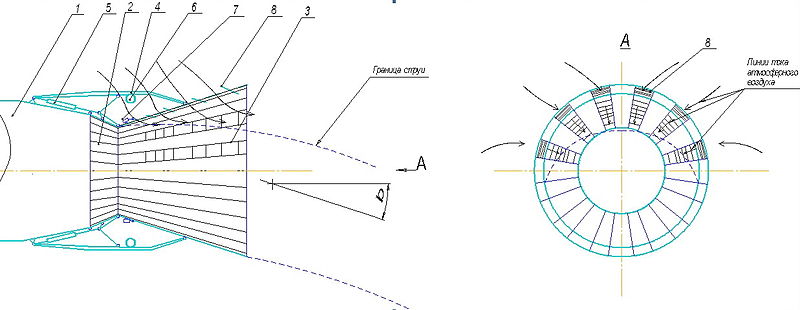
Схема и принцип действия струйного сопла показаны на рис. 5 и рис. 6.

Рис.5: Схема струйного сопла УВТ. 1 — двигатель (газогенератор двигателя); 2 — сужающаяся часть сопла с входными внутренними створками; 3 — расширяющаяся часть сопла с выходными внутренними створками; 4 — наружные кронштейны регулируемого сопла; 5 — приводы регулируемого сопла с тягами; 6 — приводы расширяющейся части сопла; 7 — приводы заслонок на створках регулируемого сопла; 8 — заслонки подвижные, управляемые.

Образование управляющих сил обеспечивается следующим порядком операций.

На первой фазе работы сопла (рис. 5) увеличивают угол отклонения створок расширяющейся части сопла — угол α установки выходных створок расширяющейся части 3 сопла.
На второй фазе (рис. 6), на режиме образования управляющих усилий на части поверхности сопла открывают заслонки 8 для поступления атмосферного воздуха на части боковой поверхности расширяющейся части сопла 3. На рис.6 показан вид А и направления втекания атмосферного воздуха через открытые отверстия с заслонками на части боковой поверхности. Переключение заслонок 8 на противоположной половине боковой расширяющейся части сопла приводит к отклонению струи и вектора тяги двигателя на угол β в противоположном направлении.

Для создания управляющих усилий в двигателе со сверхзвуковым соплом можно несколько изменить сверхзвуковую часть уже существующего сопла. Эта относительно несложная модернизация требует минимального изменения основных деталей и узлов исходного, штатного сопла.

При проектировании большая часть (до 70 %) узлов и деталей модуля сопла могут не изменяться: фланец крепления к корпусу двигателя, основной корпус, основные гидроприводы с узлами крепления, рычагами и кронштейнами, а также створки критического сечения. Изменяются конструкции надстворок и проставок расширяющейся части сопла, длина которых увеличивается, и в которых были выполнены отверстия с поворотными заслонками и гидроприводами. Кроме этого изменяется конструкция внешних створок, а пневмоцилиндры для них заменяются гидроцилиндрами, с рабочим давлением до 10 МПа (100 кг/см2).

Уменьшенная статическая устойчивость

Самолет статически устойчив, если после отклонения он возвращается к первоначальному сбалансированному состоянию. Положительная продольная статическая устойчивость является склонностью самолета возвращаться в устойчивое состояние после отклонения по тангажу. При положительной устойчивости точка приложения подъемной силы расположена в некоторой точке (аэродинамический центр) позади центра тяжести, вследствие чего увеличение подъемной силы создает момент тангажа для уменьшения угла атаки.

Для балансировки устойчивого самолета стабилизатор нагружается для противодействия опрокидывающему моменту, вызванному подъемной силой, действующей позади центра тяжести. Эта нагрузка создает ненужное балансировочное сопротивление и снижает общую подъемную силу самолета. Крыло должно быть увеличено для компенсации с последующим увеличением сопротивления.

Если продольная статическая устойчивость уменьшается – аэродинамический центр сдвигается ближе к центру тяжести – нагрузка стабилизатора уменьшается, но после возмущения возвращение в устойчивое состояние замедляется. Если подъемная сила перемещается в положение перед центром тяжести, то самолет становится продольно неустойчивым, и любое отклонение может привести к мгновенному кабрированию.

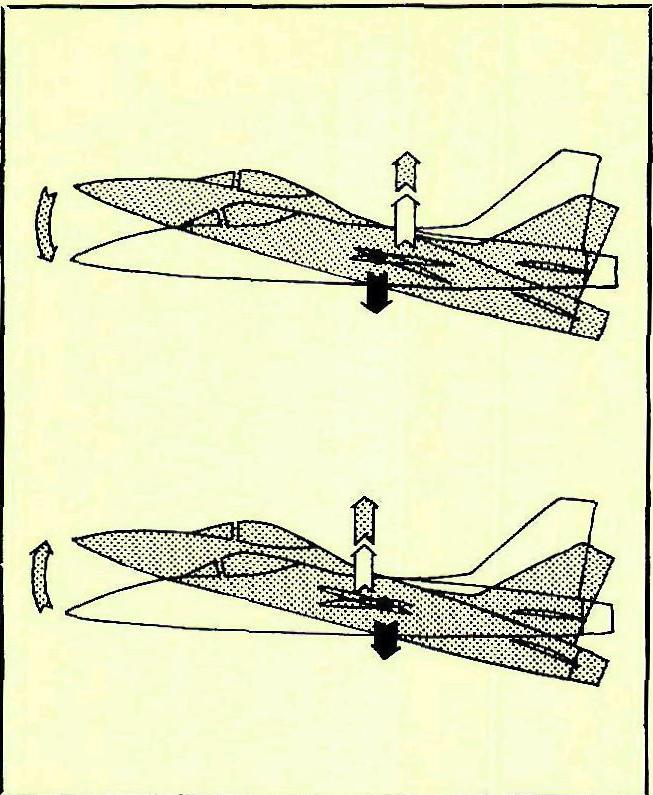
самолеты устойчивый (вверху) по сравнению с неустойчивым (внизу). У верхнего самолета аэродинамический центр позади центра тяжести, поэтому дополнительная подъемная сила опускает нос вниз. У нижнего неустойчивого самолета аэродинамический центр расположен перед центром тяжести, поэтому любое увеличение подъемной силы тянет нос самолета вверх вплоть до сваливания самолета

Загрузка стабилизатора сбалансирует неустойчивый самолет и увеличит общую подъемную силу. Крыло может быть уменьшено вместе со снижением сопротивления, требуемой тяги, размеров двигателей, емкости топливных баков, общего полетного веса, размеров крыла и т.д., в результате чего возможно сокращение размеров на 15% по сравнению со статически устойчивым истребителем.

Однако самолет без естественной устойчивости должен надежно управляться в течение всего времени, поскольку вызванный отклонением момент может развиться до того как пилот успеет среагировать. Устойчивость должна восстанавливаться автоматически активной системой управления полетом, способной почти мгновенно воспринимать и противодействовать дестабилизирующие отклонения.

Степень устойчивости или неустойчивости определяется расстоянием между аэродинамическим центром, расположенным впереди или позади центра тяжести, и самим центром тяжести, выраженным в процентах от средней аэродинамической хорды. Планируется создать конфигурацию с продольной статической неустойчивостью в 40%.

Оснащенные ПГО неустойчивые самолеты кажутся противоречием. Конечно, ведь ПГО должно создавать нагрузку для сбалансирования истребителя? Однако добавление ПГО перемещает аэродинамический центр далеко вперед от центра тяжести, делая самолет неустойчивым. Закрылки крыла используются для триммирования, которое не только увеличивает подъемную силу, но и, поскольку распределение давления улучшается, уменьшает сопротивление.

Длина вектора (в чем измеряется, как посчитать)

Длину вектора (его модуль) обозначают так:

\( \left| \vec{a} \right| \) – длина вектора \( \vec{a} \).

Как вычислить длину вектора по его координатам

Когда известны координаты вектора, его длину считают так:

\( a_{x} \) и \( a_{y} \) — это числа, координаты вектора \( \vec{a} \)

Для двухмерного вектора:

Для трехмерного вектора:

Как вычислить длину вектора с помощью рисунка

Если вектор нарисован на клетчатой бумаге, длину считаем так:

1). Если вектор лежит на линиях клеточек тетради:

— считаем количество клеточек.

Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.

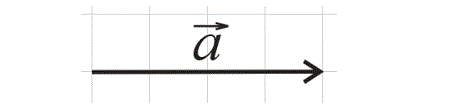Рис. 4. Вектор располагается вдоль линий, на листке в клетку

2). Если вектор не лежит вдоль линий:

— проводим вертикаль и горизонталь пунктиром.

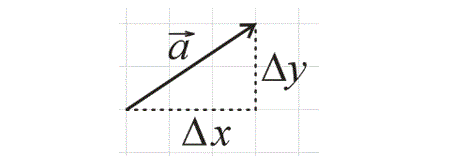Рис. 5. Вектор не расположен вдоль линий, разграничивающих листок в клетку

\( \Delta x \) — горизонталь; \( \Delta y \) — вертикаль;

— затем применяем формулу:

Ссылки [ править ]

^ «AA-11 ARCHER R-73» . Проверено 27 марта 2014 .
^ a b Джордж П. Саттон, Оскар Библарц, Элементы движения ракеты , 7-е издание.
^ Майкл Д. Гриффин и Джеймс Р. Френч, Дизайн космического корабля , второе издание.
^ «Многоразовый твердотопливный ракетный двигатель — достижения, уроки и культура успеха» . ntrs.nasa.gov . Проверено 26 февраля 2015 года .
^ a b «Разработки противотанковых управляемых ракет» . Проверено 27 марта 2014 .
^ «Боевая машина Tor 9A330» . Государственная компания «УКРОБОРОНСЕРВИС» . Проверено 27 марта 2014 .
^ «С-400 СА-20 Триумф» . Федерация американских ученых . Проверено 27 марта 2014 .
^ Mowthorpe, Сес (1998). Боевые сумки: британские дирижабли времен Первой мировой войны . Wrens Park. п. 11. ISBN 0-905778-13-8.
Перейти ↑ Abbott, Patrick (1989). Британский дирижабль в состоянии войны . Теренс Далтон. п. 84. ISBN
0-86138-073-8.
^ «ЗАПАСНОЕ ИЗОБРАЖЕНИЕ — Концепция двигателя с векторной тягой и отклонением реактивной струи 1949 года, разработанная www.DIOMEDIA.com» . Диомедия .
^ PJ Yagle; Д. Н. Миллер; КБ Гинн; Дж. В. Хамстра (2001). «Демонстрация перекоса жидкостного горла для управления вектором тяги в конструктивно фиксированных соплах» . Журнал техники газовых турбин и энергетики . 123 (3): 502–508. DOI10.1115 / 1.1361109 .
^ a b c d e f g h «Сопло с вектором тяги для современных военных самолетов» Даниэль Иказа, ИТП, представленный на симпозиуме НАТО R&T Организации, Брауншвейг, Германия, 8–11 мая 2000 г.
^ a b c d «Разработка интегрированного управления движением в полете на F-35B» Уокер, Вурт, Фуллер, AIAA 2013-44243, AIAA Aviation, 12–14 августа 2013 г., Лос-Анджелес, Калифорния, Международная конференция по лифтовой системе, 2013 г. »
^ «X-Planes, Джей Миллер, Aerofax Inc. для Orion Books, ISBN 0-517-56749-0 , Глава 18, The Bell X-14
^ «Силовая установка для самолета с вертикальным и коротким взлетом и посадкой» Bevilaqua and Shumpert, патент США № 5,209,428
^ a b «Выбор сопла и критерии проектирования» Гамбелл, Террелл, ДеФранческо, AIAA 2004-3923
^ a b c «Экспериментальное исследование осесимметричного сопла с гидравлическим вектором тяги с двумя горловинами для применения в сверхзвуковых самолетах» Фламм, Дир, Мейсон, Берриер, Джонсон, https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa .gov / 20070030933.pdf
^ Б «F-35B Lightning II Три подшипника Поворотные сопла — Код One Magazine» . codeonemagazine.com .
^ «Форсунка с регулируемым вектором для реактивных двигателей» Джонсон, Патент США 3,260,049
^ «Факты о F-22 Raptor». ВВС США , март 2009 г. Дата обращения: 10 июля 2014 г.
^ «Воздушная атака — Истребители и многое другое» . www.air-attack.com . Архивировано из оригинала на 2010-09-17.
^ a b Гал-Ор, Бенджамин (2011). «Будущие реактивные технологии». Международный журнал турбо- и реактивных двигателей . онлайн. 28 : 1–29. ISSN 2191-0332 .
^ a b Sweetmano, Билл (1999). Joint Strike Fighter: Boeing X-32 против Lockheed Martin X-35 . Серия Enthusiast Color. MBI. ISBN 0-7603-0628-1.
^ Бархэм, Роберт (июнь 1994). «Маневрирование с помощью вектора тяги опытного образца перспективного тактического истребителя YF-22» . Материалы конференции по летным испытаниям, проводимой раз в два года AIAA . Хилтон-Хед, Южная Каролина. AIAA-94-2105-CP . Дата обращения 14 мая 2020 .

8. Уилсон, Эрих А., «Введение в авиационные сопла с вектором тяги», ISBN 978-3-659-41265-3

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта

И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если , то . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Активные элементы управления

Основными элементами активной системы управления являются: датчики измерения контрольных входов, датчики движения для определения реакции самолёта на управляющее действия, высокоскоростные компьютеры и рулевые машинки. Связь между этими компонентами осуществляется посредством электрических импульсов в случае электродистанционной системы управления или по волоконно-оптическим путям в случае электрооптической системы управления.

Компьютер сравнивает отклик самолёта с запросом пилота и отклоняет поверхности управления, удаляя рассогласование. Невостребованные движения парируются автоматически. Отклики самолета на управляемые или неуправляемые возмущения определяются программным обеспечением в цифровых программируемых ЭВМ системы управления полётом.

Преимущества активной системы управления включают в себя:

искусственную устойчивость (неустойчивость с сопротивлением расходящимся движениям, благодаря чему можно уменьшить естественную устойчивость самолета и получить ничем не ограниченную маневренность),
автоматическую защиту от превышения аэродинамических ограничений и допустимых нагрузок на конструкцию,
предотвращение штопора посредством обнуления контрольных входов при приближении к ограничениям.

Другие преимущества включают:

демпфирование воздушных порывов (повышение низкого уровня плавности движения путем обнаружения порывов воздуха и отклонением управляющих поверхностей для уменьшения отклика самолета),
регулирование манёвренной нагрузки (передача подъемной силы к внутренним частям крыла для уменьшения изгиба крыла,
подавление флаттера.

Эти преимущества увеличивают срок службы планера за счет снижения износа конструкции.

концепт истребителя 1990 года компании Grumman выполняет крейсерский сверхзвуковой полет на высокой скорости и с большой дальности выпускает ракету класса воздух-земля, оставаясь при этом на расстоянии и избегая обнаружения и наведения на фоне земли ракет земля-воздух

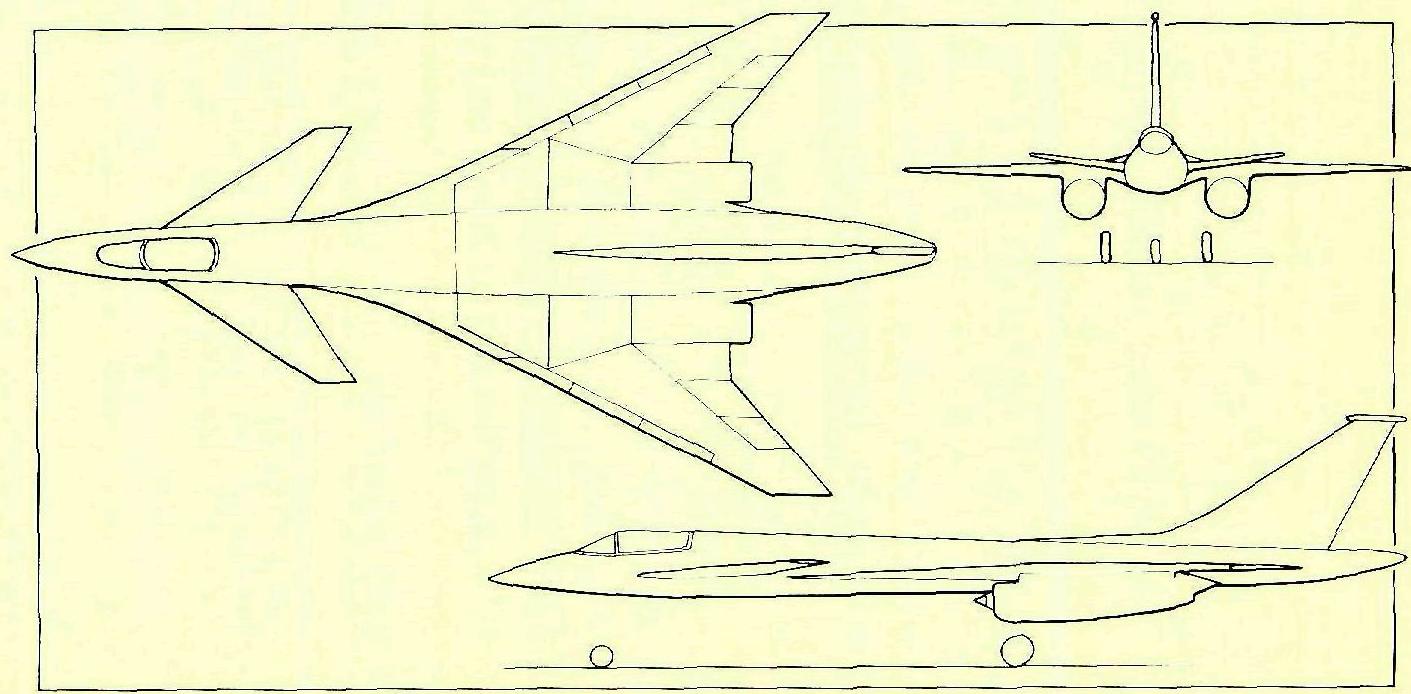
концепт истребителя 1990 года компании Grumman: длина 77,8 футов (23,71 м), вес 51500 фунтов (23360 кг)

Полная зависимость от активной системы управления (без резервных механических связей) требует высокой работоспособности системы. Способность выдерживать два схожих отказа в работе без снижения эффективности функционирования системы и надежность наработки в 107 летных часов на один катастрофический отказ оборудования требует мультиплексирования – нескольких резервных линий управления.

Большинство существующих систем четырехкратные, однако передачу цифровых данных и более интенсивный самоконтроль легче осуществить системой с тройным резервированием. Поскольку алгоритмы управления хранятся в виде программного обеспечения, то поведение самолета в полете может быть изменено (на основе летных испытаний или опыта работы) путем перепрограммирования компьютеров.

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Что такое искусственный интеллект

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

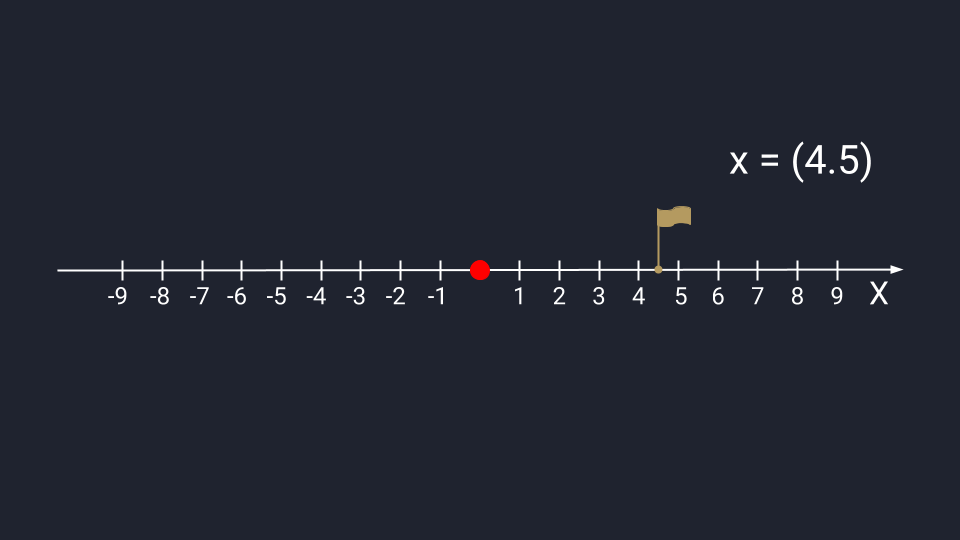Графическое представление скаляра. Записывается в круглых скобках

Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

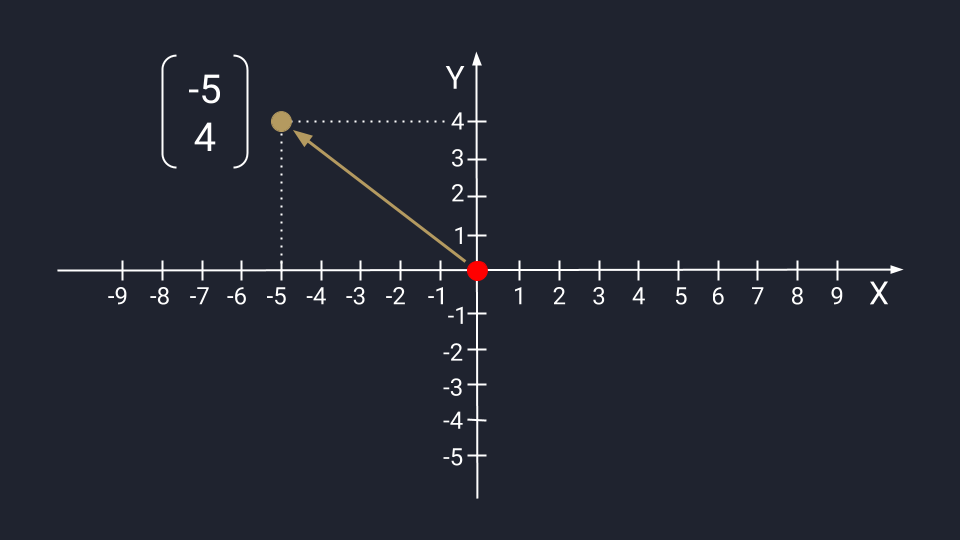Графическое представление числового вектора в двух измерениях

Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

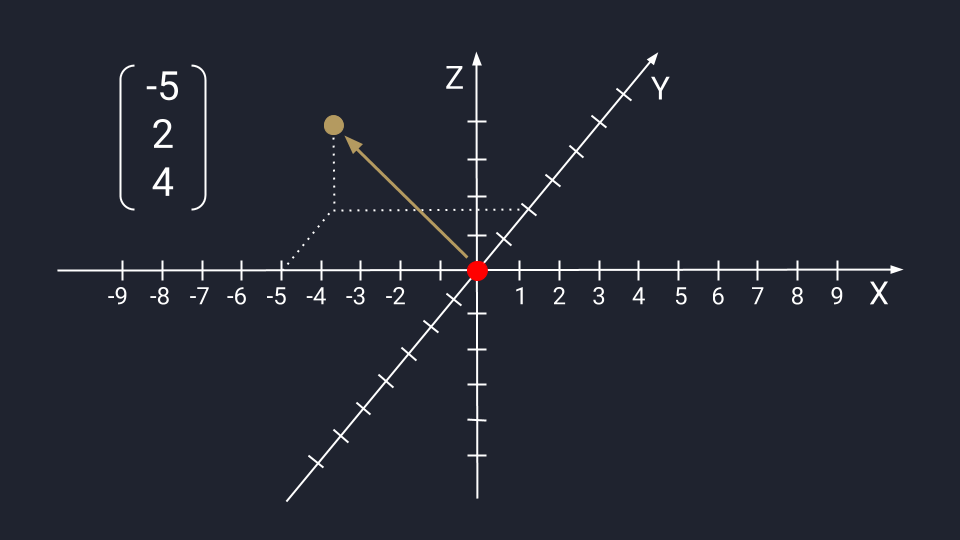Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке

Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

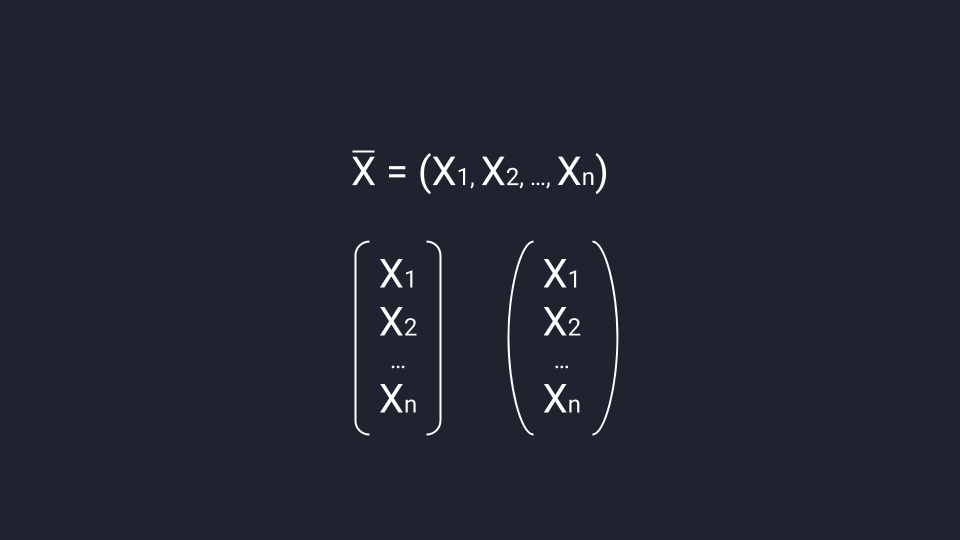Способы записи вектора

Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Что такое вектор

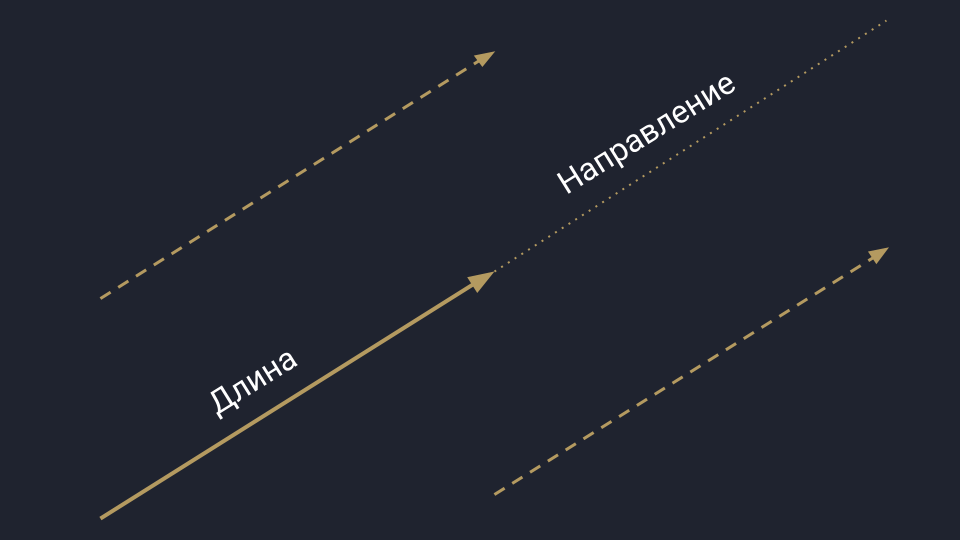
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

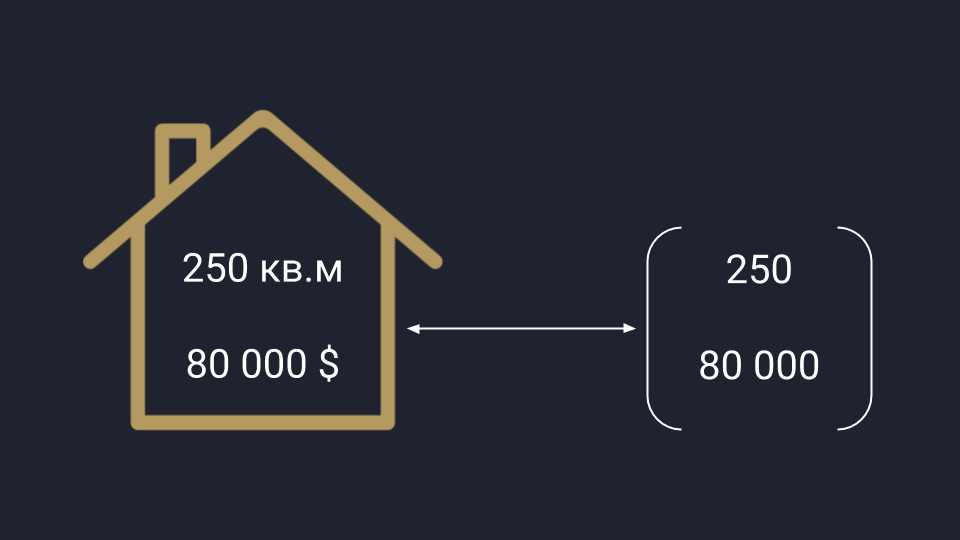
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

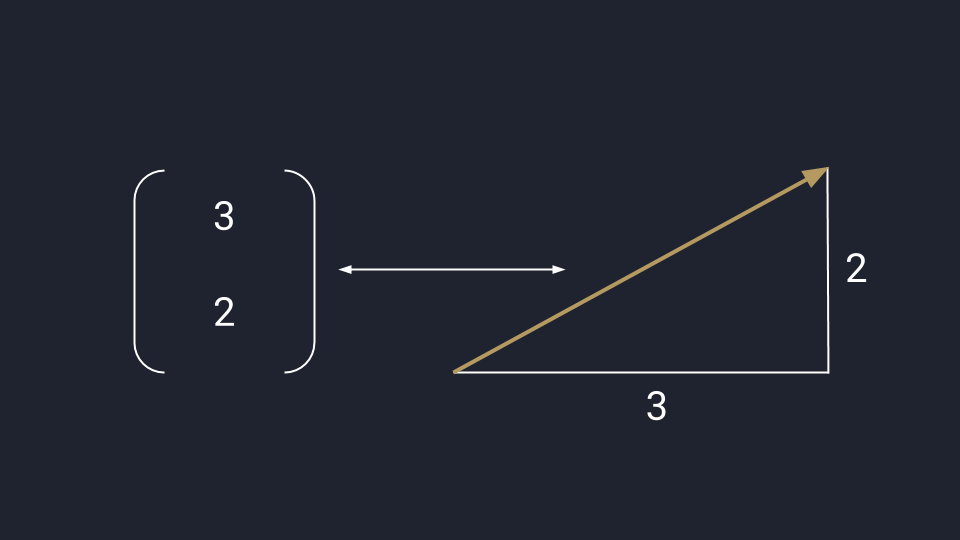
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

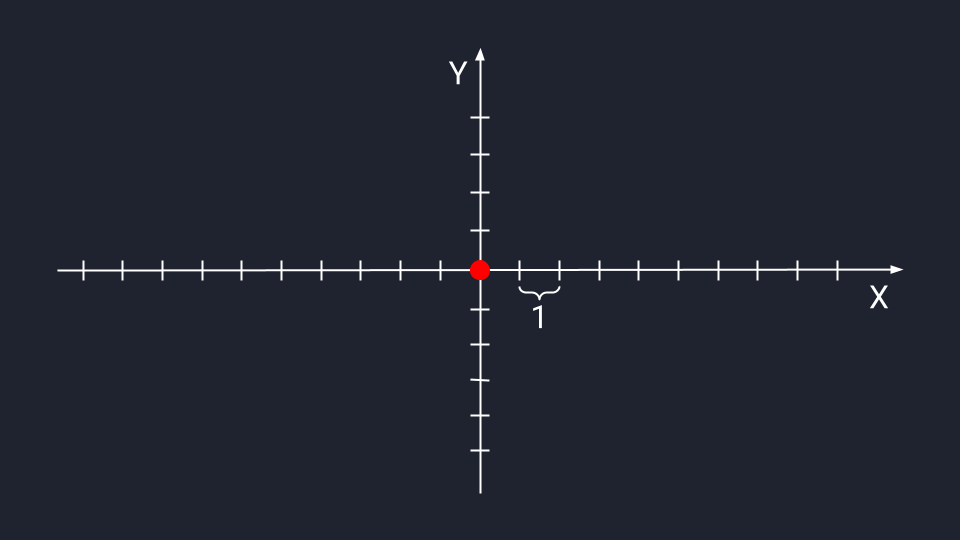Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Система управления вектором тяги

Стабилизация положения осей ЛА в пространстве и угол θ_к конечного участка активного полета ЛА обеспечиваются системой управления вектором тяги.

Газовые рули (рис. 6.5, а), выполненные из жаропрочного графита, изменяют направление струи газов на выходе из сопла двигателя при помощи поворотного устройства. Недостаток этого способа состоит в том, что установленные в поток газов на выходе из сопла рули создают, во-первых, постоянное сопротивление газовому потоку. Кроме того, за время работы двигателя, во-вторых, поверхность газовых рулей выгорает примерно на половину от первоначальной.

Этого недостатка можно избежать установкой на срезе сопла периферийных рулей (рис. 6.5, б), которые управляют вектором тяги за счет погружения щитковой поверхности руля в поток газа на срезе сопла двигателя. В нейтральном положении периферийные рули не создают сопротивления газовому потоку.

Поворот камеры или сопла. Вместо поворота камеры возможен поворот только сопла двигателя (рис. 6.5, в) или тороидального дефлектора, установленного на срезе сопла (рис. 6.5, г), или вращение сопла с косым срезом (рис. 6.5, д).

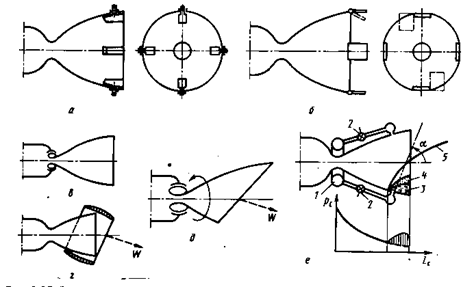Рис. 6.5. Возможные способы управления вектором тяги ЖРДУ

Вдув газа в закритическую часть сопла. Особого внимания заслуживает способ изменения вектора тяги с помощью вдува в закритическую часть сопла жидкости или газа (рис. 6.5, е). Жидкость (или газ) размещается в баллоне 1 и по команде системы управления через клапаны 2 поступает с небольшим избыточным давлением в расширяющуюся часть сопла 3 под углом α. Вблизи стенки сопла, на границе сверхзвукового потока и паровой фазы жидкости 4 (или газа), реализуется скачок уплотнения 5. За скачком уплотнения образуется область повышенного давления (на рис. 6.5, е график Р_с=f(l_c)), где происходит отклонение газовой струи в сторону оси сопла, которое вызывает отклонение всего газового потока и создает тем самым эксцентриситет тяги сопла с направлением, противоположным отклонению газового потока. При вдуве 1% расхода жидкости по отношению ко всему расходу газов через сопло возникает поперечная составляющая тяги, равная 0,5% от суммарной продольной тяги двигателя. Таким образом, вдув газа или жидкости в закритическую часть сопла применяется для точного (прецизионного) управления вектором тяги.

Перспективным является также способ управления вектором тяги за счет перераспределения расходов топлива между жестко закрепленными на ЛА камерами в многокамерной двигательной установке. Однако широкое применение этого способа сдерживается техническими трудностями реализации регуляторов перераспределения расходов топлива с одновременным сохранением соотношения компонентов топлива, организацией их взаимодействия с системами РКС и СОБ и одновременным ограничением глубины изменения режимов работы камер двигателя.

Как указать направление вектора

Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.

Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.

Для двумерного вектора

Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:

угол \( \alpha \) между вектором и горизонталью (осью Ox),
или угол \( \beta \) вежду вектором и вертикалью (осью Oy).

Рис. 6. Углы между вектором и осями на плоскости

Словами указать направление вектора можно так:

вектор длиной 5 единиц направлен под углом 30 градусов к горизонтали;
Или же: вектор длиной 5 единиц направлен под углом 60 градусов к вертикали.

Такой способ указания координат используют в полярной системе координат.

Для трехмерного вектора

Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.

угол между вектором и осью Oz;
и один из углов: между вектором и осью Oy, или между вектором и осью Ox;

Такой способ указания координат используют в сферической системе координат.

Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).

Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.

Для указания сферических координат принято использовать:

длину вектора,
угол между осью Ox и вектором и
угол между осью Oz и вектором.